【題目】某醫療器械公司在全國共有
個銷售點，總公司每年會根據每個銷售點的年銷量進行評價分析.規定每個銷售點的年銷售任務為一萬四千臺器械.根據這個銷售點的年銷量繪制出如下的頻率分布直方圖.
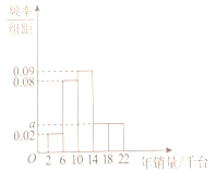
（1）完成年銷售任務的銷售點有多少個？
（2）若用分層抽樣的方法從這個銷售點中抽取容量為
的樣本，求該五組
，
，
，
，
，（單位：千臺）中每組分別應抽取的銷售點數量.
（3）在（2）的條件下，從前兩組，中的銷售點隨機選取
個，記這個銷售點在中的個數為
，求的分布列和期望.
探究與鞏固河南科學技術出版社系列答案科目：高中數學 來源： 題型：
【題目】對于由2n個質數組成的集合
，可將其元素兩兩搭配成n個乘積，得到一個n元集.若
與
是由此得到的兩個n元集，其中， 
，且
，則稱集合對{A ,B}是由M炮制成的一幅“對聯”(如由四元集{a,b,c,d}可炮制成三幅對聯:
.
求六元質數集M={a,b,c,d,e,f}所能炮制成的對聯數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某生產基地有五臺機器，現有五項工作待完成，每臺機器完成每項工作后獲得的效益值如表所示.若每臺機器只完成一項工作，且完成五項工作后獲得的效益值總和最大，則下列敘述：①甲只能承擔第四項工作；②乙不能承擔第二項工作；③丙可以不承擔第三項工作；④丁可以承擔第三項工作；其中錯誤的是______.
一 | 二 | 三 | 四 | 五 | |
甲 | 15 | 17 | 14 | 17 | 15 |
乙 | 22 | 23 | 21 | 20 | 20 |
丙 | 9 | 13 | 14 | 12 | 10 |
丁 | 7 | 9 | 11 | 9 | 11 |
戊 | 13 | 15 | 14 | 15 | 11 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
經過
兩點，且圓心在直線
上．
（1）求圓的方程；
（2）已知過點
的直線
與圓相交截得的弦長為
，求直線的方程；
（3）已知點
，在平面內是否存在異于點
的定點
，對于圓上的任意動點
，都有
為定值?若存在求出定點的坐標，若不存在說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
指數是用體重公斤數除以身高米數的平方得出的數字，是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言，當數值大于或等于20.5時，我們說體重較重，當數值小于20.5時，我們說體重較輕，身高大于或等于
我們說身高較高，身高小于170cm我們說身高較矮.
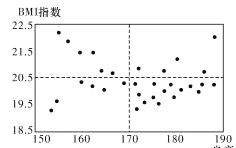
（1）已知某高中共有32名男體育特長生，其身高與
指數的數據如散點圖，請根據所得信息，完成下述列聯表，并判斷是否有
的把握認為男生的身高對指數有影響.
身高較矮 | 身高較高 | 合計 | |
體重較輕 | |||
體重較重 | |||
合計 |
（2）①從上述32名男體育特長生中隨機選取8名，其身高和體重的數據如表所示：
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根據最小二乘法的思想與公式求得線性回歸方程為
.利用已經求得的線性回歸方程，請完善下列殘差表，并求解釋變量（身高）對于預報變量（體重）變化的貢獻值（保留兩位有效數字）
；
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
殘差 | 0.1 | 0.3 | 0.9 |
|
|
②通過殘差分析，對于殘差的最大（絕對值）的那組數據，需要確認在樣本點的采集中是否有人為的錯誤，已知通過重新采集發現，該組數據的體重應該為
.請重新根據最最小二乘法的思想與公式，求出男體育特長生的身高與體重的線性回歸方程.
（參考公式）
，
，
，
，
.
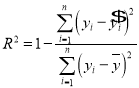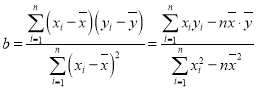（參考數據）
，
，
，
，
.
0.10
0.05
0.01
0.005
2.706
3.811
6.635
7.879
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將高二（1）班的四個同學分到語文、數學、英語三個興趣小組，每個興趣小組至少有一名同學的分配方法有多少種？下列結論正確的有（ ）
A.
B.
C.
D.18
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
