
【題目】已知![]() ,n∈N*.
,n∈N*.
(1)設f(x)=a0+a1x+a2x2+…+anxn,
①求a0+a1+a2+…+an;
②若在a0,a1,a2,…,an中,唯一的最大的數是a4,試求n的值;
(2)設f(x)=b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n,求![]() .
.
【答案】(1)①![]() ;②n=12或13;(2)
;②n=12或13;(2)![]() (2n+1﹣2﹣n)
(2n+1﹣2﹣n)
【解析】
(1)①可令x=1,代入計算可得所求和;②可得f(x)=(x+2)n=(2+x)n的通項公式,ar最大即為ar≥ar﹣1,且ar≥ar+1,化簡計算,結合不等式的解,可得所求值;
(2)由f(x)=[1+(x+1)]n,可得br=C![]() ,r=0,1,…,n,推得
,r=0,1,…,n,推得![]() ,再由二項式定理,計算可得所求和.
,再由二項式定理,計算可得所求和.
解:(1)①由(x+2)n=a0+a1x+a2x2+…+anxn,
可令x=1,可得3n=a0+a1+a2+…+an,
即a0+a1+a2+…+an=3n;
②f(x)=(x+2)n=(2+x)n,
可得ar![]() 2n﹣rxr,r=0,1,…,n,
2n﹣rxr,r=0,1,…,n,
若在a0,a1,a2,…,an中,ar最大,
可得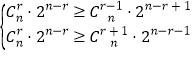 ,即為
,即為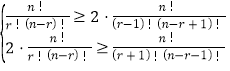 ,
,
化為![]() ,由于r=4時為a4唯一的最大值,
,由于r=4時為a4唯一的最大值,
可得n=12,13;
(2)由f(x)=b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n,
且f(x)=[1+(x+1)]n,可得br=C![]() ,r=0,1,…,n,
,r=0,1,…,n,
則![]() ,
,
由![]()
![]()
![]() ,
,
則![]() (C
(C![]() )
)![]() (2n+1﹣2﹣n).
(2n+1﹣2﹣n).


科目:高中數學 來源: 題型:
【題目】![]() 指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當
指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當![]() 數值大于或等于20.5時,我們說體重較重,當
數值大于或等于20.5時,我們說體重較重,當![]() 數值小于20.5時,我們說體重較輕,身高大于或等于
數值小于20.5時,我們說體重較輕,身高大于或等于![]() 我們說身高較高,身高小于170cm我們說身高較矮.
我們說身高較高,身高小于170cm我們說身高較矮.
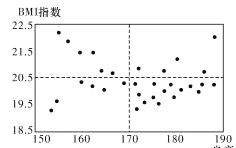
(1)已知某高中共有32名男體育特長生,其身高與![]() 指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有
指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有![]() 的把握認為男生的身高對
的把握認為男生的身高對![]() 指數有影響.
指數有影響.
身高較矮 | 身高較高 | 合計 | |
體重較輕 | |||
體重較重 | |||
合計 |
(2)①從上述32名男體育特長生中隨機選取8名,其身高和體重的數據如表所示:
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根據最小二乘法的思想與公式求得線性回歸方程為![]() .利用已經求得的線性回歸方程,請完善下列殘差表,并求解釋變量(身高)對于預報變量(體重)變化的貢獻值(保留兩位有效數字)
.利用已經求得的線性回歸方程,請完善下列殘差表,并求解釋變量(身高)對于預報變量(體重)變化的貢獻值(保留兩位有效數字)![]() ;
;
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
殘差 | 0.1 | 0.3 | 0.9 |
|
|
②通過殘差分析,對于殘差的最大(絕對值)的那組數據,需要確認在樣本點的采集中是否有人為的錯誤,已知通過重新采集發現,該組數據的體重應該為![]() .請重新根據最最小二乘法的思想與公式,求出男體育特長生的身高與體重的線性回歸方程.
.請重新根據最最小二乘法的思想與公式,求出男體育特長生的身高與體重的線性回歸方程.
(參考公式)
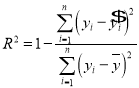 ,
,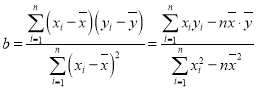 ,
,![]() ,
,![]() ,
,![]() .
.
(參考數據)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
0.10
0.05
0.01
0.005
![]()
2.706
3.811
6.635
7.879
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將高二(1)班的四個同學分到語文、數學、英語三個興趣小組,每個興趣小組至少有一名同學的分配方法有多少種?下列結論正確的有( )
A.![]() B.
B.![]()
C.![]() D.18
D.18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為內角A,B,C的對邊,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面積S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動,點
軸滾動,點![]() 恰好經過原點.設頂點
恰好經過原點.設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數
,則對函數![]() 有下列判斷:①函數
有下列判斷:①函數![]() 是偶函數;②對任意的
是偶函數;②對任意的![]() ,都有
,都有![]() ;③函數
;③函數![]() 在區間
在區間![]() 上單調遞減;④函數
上單調遞減;④函數![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判斷正確的序號是__________.
.其中判斷正確的序號是__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】指出下列命題是全稱量詞命題還是存在量詞命題,并判斷它們的真假.
(1)x∈N,2x+1是奇數;
(2)存在一個x∈R,使![]() =0;
=0;
(3)對任意實數a,|a|>0;
(4)有一個角α,使sinα=![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學志愿者協會有6名男同學,4名女同學,在這10名同學中,3名同學來自數學學院,其余7名同學來自物理﹑化學等其他互不相同的七個學院,現從這10名同學中隨機選取3名同學,到希望小學進行支教活動(每位同學被選到的可能性相同).
(1)求選出的3名同學是來自互不相同學院的概率;
(2)設![]() 為選出的3名同學中女同學的人數,求隨機變量
為選出的3名同學中女同學的人數,求隨機變量![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com