
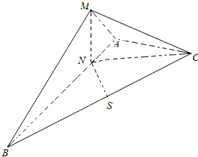
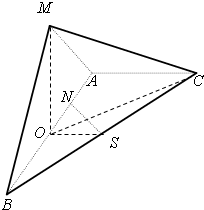
 如圖,在三棱錐M-ABC中,AB=2AC=2,
如圖,在三棱錐M-ABC中,AB=2AC=2,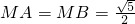 ,AB=4AN,AB⊥AC,平面MAB⊥平面ABC,S為BC中點
,AB=4AN,AB⊥AC,平面MAB⊥平面ABC,S為BC中點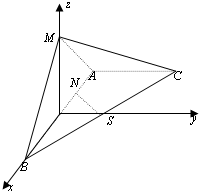
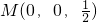 、
、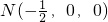 、
、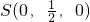
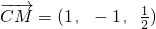 ,
,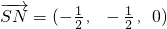
 ,∴CM⊥SN
,∴CM⊥SN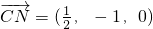 ,
,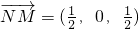
 ,則
,則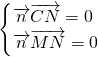 ,∴
,∴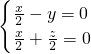

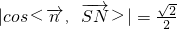 ,∴SN與平面CMN所成角為
,∴SN與平面CMN所成角為
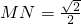
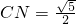
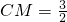 ,
,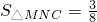
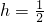
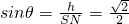

 ,證明CM⊥SN;
,證明CM⊥SN;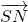 ,利用向量的夾角公式,即可求得SN與平面CMN所成角;
,利用向量的夾角公式,即可求得SN與平面CMN所成角;

科目:高中數學 來源: 題型:
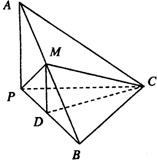 21、如圖,在三棱錐A-BPC中,AP⊥PC,AC⊥BC,M為AB中點,D為PB中點,且△PMB為正三角形,
21、如圖,在三棱錐A-BPC中,AP⊥PC,AC⊥BC,M為AB中點,D為PB中點,且△PMB為正三角形,查看答案和解析>>
科目:高中數學 來源: 題型:
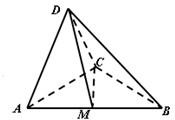 如圖,在三棱錐D-ABC中,△ADC,△ACB均為等腰直角三角形AD=CD=
如圖,在三棱錐D-ABC中,△ADC,△ACB均為等腰直角三角形AD=CD=| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
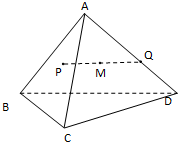 如圖,在三棱錐A-BCD中,AB,AC,AD兩兩互相垂直,AB=AC=AD=4,點P,Q分別在側面ABC棱AD上運動,PQ=2,M為線段PQ中點,當P,Q運動時,點M的軌跡把三棱錐A-BCD分成上、下兩部分的體積之比等于
如圖,在三棱錐A-BCD中,AB,AC,AD兩兩互相垂直,AB=AC=AD=4,點P,Q分別在側面ABC棱AD上運動,PQ=2,M為線段PQ中點,當P,Q運動時,點M的軌跡把三棱錐A-BCD分成上、下兩部分的體積之比等于查看答案和解析>>
科目:高中數學 來源: 題型:
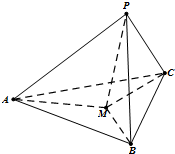 如圖,在三棱錐P-ABC中,PA,PB,PC兩兩垂直,且PA=5,PB=4,PC=3.設點M為底面ABC內一點,定義f(M)=(m,n,p),其中m,n,p分別為三棱錐M-PAB、M-PBC、M-PCA的體積.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,則正實數a的取值范圍是
如圖,在三棱錐P-ABC中,PA,PB,PC兩兩垂直,且PA=5,PB=4,PC=3.設點M為底面ABC內一點,定義f(M)=(m,n,p),其中m,n,p分別為三棱錐M-PAB、M-PBC、M-PCA的體積.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,則正實數a的取值范圍是查看答案和解析>>
科目:高中數學 來源: 題型:
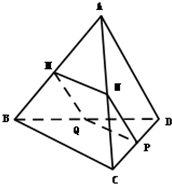 如圖,在三棱錐A-BCD中,平行于BC的平面MNPQ分別交AB、AC、CD、BD于M、N、P、Q四點,且MN=PQ.
如圖,在三棱錐A-BCD中,平行于BC的平面MNPQ分別交AB、AC、CD、BD于M、N、P、Q四點,且MN=PQ.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com