
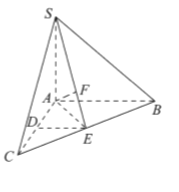
【題目】如圖,四棱錐P-ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,![]() E是PD的中點.
E是PD的中點.
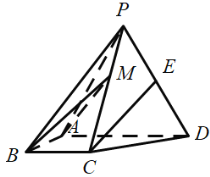
(1)證明:直線![]() 平面PAB;
平面PAB;
(2)點M在棱PC 上,且直線BM與底面ABCD所成角為![]() ,求二面角M-AB-D的余弦值.
,求二面角M-AB-D的余弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)取PA的中點F,連接EF,BF,通過證明CE∥BF,利用直線與平面平行的判定定理證明即可;
(2)利用已知條件轉化求解M到底面的距離,作出二面角的平面角,然后求解二面角MABD的余弦值即可.
(1)證明:取PA的中點F,連接EF,BF,
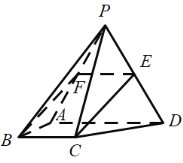
因為E是PD的中點,
所以![]() ,∠BAD=∠ABC=90°,
,∠BAD=∠ABC=90°,
∴![]() ,
,
∴BCEF是平行四邊形,可得CE∥BF,BF平面PAB,![]() 平面PAB,
平面PAB,
∴直線CE∥平面PAB;
(2)解:四棱錐PABCD中,
側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=![]() AD,
AD,
∠BAD=∠ABC=90°,E是PD的中點.
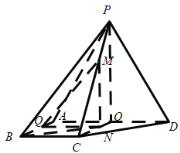
取AD的中點O,M在底面ABCD上的射影N在OC上,
設AD=2,則AB=BC=1,OP=![]() ,
,
∴∠PCO=60°,直線BM與底面ABCD所成角為45°,
可得:BN=MN,![]() ,BC=1,
,BC=1,
可得:![]() ,
,
作NQ⊥AB于Q,連接MQ,AB⊥MN,
所以∠MQN就是二面角MABD的平面角,MQ= ,
,
二面角MABD的余弦值為: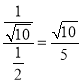 .
.


科目:高中數學 來源: 題型:
【題目】2019年4月,北京世界園藝博覽會開幕,為了保障園藝博覽會安全順利地進行,某部門將5個安保小組全部安排到指定的三個不同區域內值勤,則每個區域至少有一個安保小組的排法有( )
A.150種B.240種C.300種D.360種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,![]() 在
在![]() 上且
上且![]() .
.
(I)求證:![]() ;
;
(II)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在線段![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 與圓
與圓![]() :
: ![]() 相切,且與圓
相切,且與圓![]() :
: ![]() 相內切,記圓心
相內切,記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .設
.設![]() 為曲線
為曲線![]() 上的一個不在
上的一個不在![]() 軸上的動點,
軸上的動點, ![]() 為坐標原點,過點
為坐標原點,過點![]() 作
作![]() 的平行線交曲線
的平行線交曲線![]() 于
于![]() ,
, ![]() 兩個不同的點.
兩個不同的點.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)試探究![]() 和
和![]() 的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
(Ⅲ)記![]() 的面積為
的面積為![]() ,
, ![]() 的面積為
的面積為![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】英語老師要求學生從星期一到星期四每天學習3個英語單詞:每周五對一周內所學單詞隨機抽取若干個進行檢測(一周所學的單詞每個被抽到的可能性相同)
(1)英語老師隨機抽了![]() 個單詞進行檢測,求至少有
個單詞進行檢測,求至少有![]() 個是后兩天學習過的單詞的概率;
個是后兩天學習過的單詞的概率;
(2)某學生對后兩天所學過的單詞每個能默寫對的概率為![]() ,對前兩天所學過的單詞每個能默寫對的概率為
,對前兩天所學過的單詞每個能默寫對的概率為![]() ,若老師從后三天所學單詞中各抽取一個進行檢測,求該學生能默寫對的單詞的個數
,若老師從后三天所學單詞中各抽取一個進行檢測,求該學生能默寫對的單詞的個數![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于頂點在原點的拋物線,給出下列條件:
①焦點在y軸上;
②焦點在x軸上
③拋物線上橫坐標為1的點到焦點的距離等于6;
④拋物線的過焦點且垂直于對稱軸的弦的長為5;
⑤由原點向過焦點的某條直線作垂線,垂足坐標為(2,1)
能使拋物線方程為y2=10x的條件是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com