定義:同時滿足下列兩個條件的數(shù)列{a
n} 叫做“上凸有界數(shù)列”,①
≤an+1②a
n≤M,M是與n無關(guān)的常數(shù).
(I)若數(shù)列{a
n} 的前n項(xiàng)和為S
n,且S
n=2
n-1,試判斷數(shù)列{a
n} 是否為上凸有界數(shù)列;
(Ⅱ)若數(shù)列{b
n}是等差數(shù)列,T
n為其前n項(xiàng)和,且b
3=4,T
3=18,試證明:數(shù)列{T
n}為上凸有界數(shù)列.
(I)n=1時,a
1=s
1=2-1=1
n≥2時a
n=s
n-s
n-1=2
n-1-(2
n-1-1)=2
n-1∴a
n=2
n-1顯然a
n=2
n-1是遞增數(shù)列,故不存在常數(shù)M,使a
n≤M成立
∴數(shù)列{a
n} 不是上凸有界數(shù)列
(II)設(shè){b
n}的公差為d,則
解得b
1=8,d=-2
∴T
n=8n+
(-2)=-n
2+9n
∵
-Tn+1=
=
=
=-1<0
∴
≤Tn+1,即{T
n}滿足條件①
又T
n=-n
2+9n=-(n-
)
2+
當(dāng)n=4或5時T
n取最大值20,即T
n≤20,滿足條件②
綜上數(shù)列{T
n}為上凸有界數(shù)列
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
定義:同時滿足下列兩個條件的數(shù)列{a
n} 叫做“上凸有界數(shù)列”,①
≤an+1②a
n≤M,M是與n無關(guān)的常數(shù).
(I)若數(shù)列{a
n} 的前n項(xiàng)和為S
n,且S
n=2
n-1,試判斷數(shù)列{a
n} 是否為上凸有界數(shù)列;
(Ⅱ)若數(shù)列{b
n}是等差數(shù)列,T
n為其前n項(xiàng)和,且b
3=4,T
3=18,試證明:數(shù)列{T
n}為上凸有界數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2012-2013學(xué)年山東省濟(jì)寧市曲阜師大附中高二(上)期中數(shù)學(xué)試卷(理科)(解析版)
題型:解答題
定義:同時滿足下列兩個條件的數(shù)列{a
n} 叫做“上凸有界數(shù)列”,①
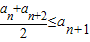
②a
n≤M,M是與n無關(guān)的常數(shù).
(I)若數(shù)列{a
n} 的前n項(xiàng)和為S
n,且S
n=2
n-1,試判斷數(shù)列{a
n} 是否為上凸有界數(shù)列;
(Ⅱ)若數(shù)列{b
n}是等差數(shù)列,T
n為其前n項(xiàng)和,且b
3=4,T
3=18,試證明:數(shù)列{T
n}為上凸有界數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2011年山東省臨沂市高考數(shù)學(xué)二模試卷(文科)(解析版)
題型:解答題
定義:同時滿足下列兩個條件的數(shù)列{a
n} 叫做“上凸有界數(shù)列”,①
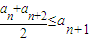
②a
n≤M,M是與n無關(guān)的常數(shù).
(I)若數(shù)列{a
n} 的前n項(xiàng)和為S
n,且S
n=2
n-1,試判斷數(shù)列{a
n} 是否為上凸有界數(shù)列;
(Ⅱ)若數(shù)列{b
n}是等差數(shù)列,T
n為其前n項(xiàng)和,且b
3=4,T
3=18,試證明:數(shù)列{T
n}為上凸有界數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2011年山東省臨沂市高考數(shù)學(xué)二模試卷(理科)(解析版)
題型:解答題
定義:同時滿足下列兩個條件的數(shù)列{a
n} 叫做“上凸有界數(shù)列”,①
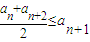
②a
n≤M,M是與n無關(guān)的常數(shù).
(I)若數(shù)列{a
n} 的前n項(xiàng)和為S
n,且S
n=2
n-1,試判斷數(shù)列{a
n} 是否為上凸有界數(shù)列;
(Ⅱ)若數(shù)列{b
n}是等差數(shù)列,T
n為其前n項(xiàng)和,且b
3=4,T
3=18,試證明:數(shù)列{T
n}為上凸有界數(shù)列.
查看答案和解析>>



 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案
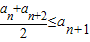 ②an≤M,M是與n無關(guān)的常數(shù).
②an≤M,M是與n無關(guān)的常數(shù).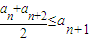 ②an≤M,M是與n無關(guān)的常數(shù).
②an≤M,M是與n無關(guān)的常數(shù).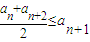 ②an≤M,M是與n無關(guān)的常數(shù).
②an≤M,M是與n無關(guān)的常數(shù).