
【題目】設函數![]() .
.
(Ⅰ)當a=1時,求曲線y=f(x)在點(0,f(0))處的切線方程;
(Ⅱ)求函數f(x)單調區間.
【答案】(Ⅰ)x﹣y+1=0.(Ⅱ)當a=0時,單調遞增區間是(﹣∞,0),單調遞減區間是(0,+∞).當0<a<1時,單調遞增區間是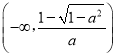 和
和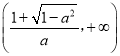 ,單調遞減區間是
,單調遞減區間是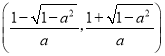 .當a≥1時,單調遞增區間是(﹣∞,+∞),無減區間.當﹣1<a<0時,單調遞減區間是
.當a≥1時,單調遞增區間是(﹣∞,+∞),無減區間.當﹣1<a<0時,單調遞減區間是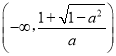 和
和 ,單調遞增區間
,單調遞增區間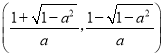 .當a≤﹣1時,單調遞減區間是(﹣∞,+∞),無增區間.
.當a≤﹣1時,單調遞減區間是(﹣∞,+∞),無增區間.
【解析】
(I)先求導數f'(x),利用導數求出在x=0處的導函數值,即為切線的斜率,則可得出切線方程.
(II)對字母a進行分類討論,再令f'(x)大于0,解不等式,可得函數的單調增區間,令導數小于0,可得函數的單調減區間.
因為![]() ,所以
,所以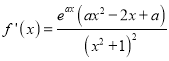 .
.
(Ⅰ)當a=1時,![]() ,
,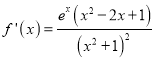 ,
,
所以f(0)=1,f'(0)=1.
所以曲線y=f(x)在點(0,f(0))處的切線方程為x﹣y+1=0.
(Ⅱ)因為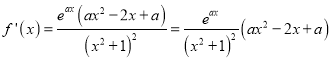 ,
,
(1)當a=0時,由f'(x)>0得x<0;由f'(x)<0得x>0.
所以函數f(x)在區間(﹣∞,0)單調遞增,在區間(0,+∞)單調遞減.
(2)當a≠0時,設g(x)=ax2﹣2x+a,方程g(x)=ax2﹣2x+a=0的判別式△=4﹣4a2=4(1﹣a)(1+a),
①當0<a<1時,此時△>0.
由f'(x)>0得![]() ,或
,或![]() ;
;
由f'(x)<0得![]() .
.
所以函數f(x)單調遞增區間是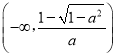 和
和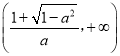 ,
,
單調遞減區間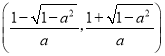 .
.
②當a≥1時,此時△≤0.所以f'(x)≥0,
所以函數f(x)單調遞增區間是(﹣∞,+∞).
③當﹣1<a<0時,此時△>0.
由f'(x)>0得![]() ;
;
由f'(x)<0得![]() ,或
,或![]() .
.
所以當﹣1<a<0時,函數f(x)單調遞減區間是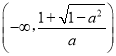 和
和 ,
,
單調遞增區間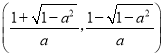 .
.
④當a≤﹣1時,此時△≤0,f'(x)≤0,所以函數f(x)單調遞減區間是(﹣∞,+∞).


科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量表得如下頻數分布表:
質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
頻數 | 6 | 26 | 38 | 22 | 8 |
(I)在答題卡上作出這些數據的頻率分布直方圖:
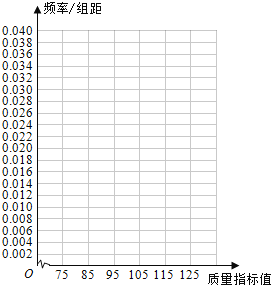
(II)估計這種產品質量指標值的平均數及方差(同一組中的數據用該組區間的中點值作代表);
(III)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于95的產品至少要占全部產品的80%”的規定?
查看答案和解析>>
科目:高中數學 來源: 題型:
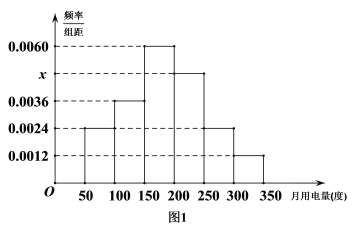
【題目】從某小區抽取50戶居民進行月用電量調查,發現其用電量都在50到350度之間,頻率分布直方圖如圖1.
A類用戶 | B類用戶 | |||||||
9 | 7 | 7 | 0 | 6 | ||||
8 | 6 | 5 | 1 | 7 | 8 | 9 | ||
9 | 8 | 2 | 8 | 5 | 6 | 7 | 8 | |
8 | 7 | 1 | 0 | 9 | 7 | 8 | 9 | |
圖2
(1)求頻率分布直方圖中![]() 的值并估計這50戶用戶的平均用電量;(2)若將用電量在區間
的值并估計這50戶用戶的平均用電量;(2)若將用電量在區間![]() 內的用戶記為
內的用戶記為![]() 類用戶,標記為低用電家庭,用電量在區間
類用戶,標記為低用電家庭,用電量在區間![]() 內的用戶記為
內的用戶記為![]() 類用戶,標記為高用電家庭,現對這兩類用戶進行問卷調查,讓其對供電服務進行打分,打分情況見莖葉圖2;若打分超過85分視為滿意,沒超過85分視為不滿意,請填寫下面列聯表,并根據列聯表判斷是否有
類用戶,標記為高用電家庭,現對這兩類用戶進行問卷調查,讓其對供電服務進行打分,打分情況見莖葉圖2;若打分超過85分視為滿意,沒超過85分視為不滿意,請填寫下面列聯表,并根據列聯表判斷是否有![]() 的把握認為“滿意度與用電量高低有關”?
的把握認為“滿意度與用電量高低有關”?
滿意 | 不滿意 | 合計 | |
| |||
| |||
合計 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
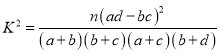 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠甲、乙兩個車間包裝同一種產品,在自動包裝傳送帶上每隔一小時抽一包產品,稱其重量(單位:克)是否合格,分別記錄抽查數據,獲得重量數據莖葉如圖所示.
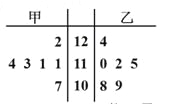
(Ⅰ)根據樣本數據,計算甲、乙兩個車間產品重量的均值與方差,并說明哪個車間的產品的重量相對穩定;
(Ⅱ)若從乙車間![]() 件樣品中隨機抽取兩件,求所抽取兩件樣品重量之差不超過
件樣品中隨機抽取兩件,求所抽取兩件樣品重量之差不超過![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經銷商經銷某種農產品,在一個銷售季度內,每售出1t該產品獲利潤500元,未售出的產品,每1t虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直圖,如右圖所示.經銷商為下一個銷售季度購進了130t該農產品.以![]() (單位:t,100≤
(單位:t,100≤![]() ≤150)表示下一個銷售季度內的市場需求量,T(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
≤150)表示下一個銷售季度內的市場需求量,T(單位:元)表示下一個銷售季度內經銷該農產品的利潤.

(Ⅰ)將T表示為![]() 的函數;
的函數;
(Ⅱ)根據直方圖估計利潤T不少于57000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 、
、![]() 是兩個小區所在地,
是兩個小區所在地,![]() 、
、![]() 到一條公路
到一條公路![]() 的垂直距離分別為
的垂直距離分別為![]()
![]() ,
,![]()
![]() ,
,![]() 兩端之間的距離為
兩端之間的距離為![]()
![]() .
.
(1)某移動公司將在![]() 之間找一點
之間找一點![]() ,在
,在![]() 處建造一個信號塔,使得
處建造一個信號塔,使得![]() 對
對![]() 、
、![]() 的張角與
的張角與![]() 對
對![]() 、
、![]() 的張角相等,試確定點
的張角相等,試確定點![]() 的位置.
的位置.
(2)環保部門將在![]() 之間找一點
之間找一點![]() ,在
,在![]() 處建造一個垃圾處理廠,使得
處建造一個垃圾處理廠,使得![]() 對
對![]() 、
、![]() 所張角最大,試確定點
所張角最大,試確定點![]() 的位置.
的位置.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com