
【題目】已知函數(shù)![]() (其中
(其中![]() 為自然對數(shù)的底數(shù),
為自然對數(shù)的底數(shù),![]() ).
).
(1)若![]() 是函數(shù)
是函數(shù)![]() 的極值點(diǎn),求
的極值點(diǎn),求![]() 的值,并求
的值,并求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 時都有
時都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;
;![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() ;
;
(2)![]()
【解析】
(1)由極值點(diǎn)可知![]() ,從而求得
,從而求得![]() ;根據(jù)導(dǎo)函數(shù)的正負(fù)即可確定
;根據(jù)導(dǎo)函數(shù)的正負(fù)即可確定![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)求導(dǎo)后得到導(dǎo)函數(shù);當(dāng)![]() 和
和![]() 時,可根據(jù)導(dǎo)函數(shù)正負(fù)確定
時,可根據(jù)導(dǎo)函數(shù)正負(fù)確定![]() 單調(diào)遞增,從而
單調(diào)遞增,從而![]() ,滿足題意;當(dāng)
,滿足題意;當(dāng)![]() 時,由零點(diǎn)存在定理可知存在
時,由零點(diǎn)存在定理可知存在![]() ,使得
,使得![]() 時,
時,![]() ,由單調(diào)性可知
,由單調(diào)性可知![]() 不恒成立;從而得到所求范圍.
不恒成立;從而得到所求范圍.
(1)由![]() 得:
得:![]() 定義域為
定義域為![]() ,
,![]()
![]() 是
是![]() 的極值點(diǎn)
的極值點(diǎn) ![]() ,解得:
,解得:![]()
此時![]() ,
,![]()
當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞增
單調(diào)遞增
![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]()
(2)![]() ,
,![]()
①當(dāng)![]() 時,
時,![]() 恒成立
恒成立 ![]() 單調(diào)遞增
單調(diào)遞增 ![]() ,滿足題意
,滿足題意
②當(dāng)![]() 時,
時,![]() 是
是![]() 上的增函數(shù),且
上的增函數(shù),且![]()
若![]() ,即
,即![]() ,則
,則![]() 且不恒等于
且不恒等于![]()
![]() 單調(diào)遞增
單調(diào)遞增 ![]() ,滿足題意
,滿足題意
若![]() ,即
,即![]() ,
,![]() ,
,![]()
![]() 存在
存在![]() ,使得
,使得![]()
當(dāng)![]() 時,
時,![]() ,則
,則![]() 單調(diào)遞減
單調(diào)遞減 ![]()
即![]() 不恒成立,不合題意
不恒成立,不合題意
綜上所述:實數(shù)![]() 的取值范圍為
的取值范圍為![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C1的圓心在坐標(biāo)原點(diǎn)O,且恰好與直線![]() 相切.
相切.
(Ⅰ)求圓C1的標(biāo)準(zhǔn)方程;
(Ⅱ)設(shè)點(diǎn)A為圓上一動點(diǎn),AN垂直于x軸于點(diǎn)N,若動點(diǎn)Q滿足![]()
(其中m為非零常數(shù)),試求動點(diǎn)Q的軌跡方程;
(Ⅲ)在(Ⅱ)的結(jié)論下,當(dāng)m=![]() 時,得到動點(diǎn)Q的軌跡為曲線C,與l1垂直的直線l與曲線C交于B,D兩點(diǎn),求△OBD面積的最大值.
時,得到動點(diǎn)Q的軌跡為曲線C,與l1垂直的直線l與曲線C交于B,D兩點(diǎn),求△OBD面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在棱長為1的正方體![]() 中,動點(diǎn)
中,動點(diǎn)![]() 在線段
在線段![]() 上運(yùn)動,且有
上運(yùn)動,且有![]() .
.

(1)若![]() ,求證:
,求證:![]() ;
;
(2)若二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]()
![]() 討論
討論![]() 的單調(diào)性;
的單調(diào)性;
![]() 若
若![]() 是
是![]() 的極值點(diǎn),且曲線
的極值點(diǎn),且曲線![]() 在兩點(diǎn)
在兩點(diǎn)![]()
![]() 處的切線相互平行,這兩條切線在
處的切線相互平行,這兩條切線在![]() 軸上的截距分別為
軸上的截距分別為![]() ,求
,求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
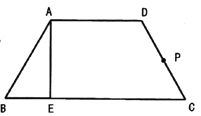
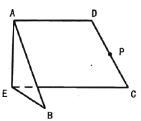
【題目】如圖,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 上一點(diǎn),且
上一點(diǎn),且![]() ,
,![]() 為
為![]() 的中點(diǎn).沿
的中點(diǎn).沿![]() 將梯形折成大小為
將梯形折成大小為![]() 的二面角
的二面角![]() ,若
,若![]() 內(nèi)(含邊界)存在一點(diǎn)
內(nèi)(含邊界)存在一點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ,則
,則![]() 的取值范圍是__________.
的取值范圍是__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】箱子里有16張撲克牌:紅桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方塊
、6、5、4,方塊![]() 、5,老師從這16張牌中挑出一張牌來,并把這張牌的點(diǎn)數(shù)告訴了學(xué)生甲,把這張牌的花色告訴了學(xué)生乙,這時,老師問學(xué)生甲和學(xué)生乙:你們能從已知的點(diǎn)數(shù)或花色中推知這張牌是什么牌嗎?于是,老師聽到了如下的對話:學(xué)生甲:我不知道這張牌;學(xué)生乙:我知道你不知道這張牌;學(xué)生甲:現(xiàn)在我知道這張牌了;學(xué)生乙:我也知道了.則這張牌是( )
、5,老師從這16張牌中挑出一張牌來,并把這張牌的點(diǎn)數(shù)告訴了學(xué)生甲,把這張牌的花色告訴了學(xué)生乙,這時,老師問學(xué)生甲和學(xué)生乙:你們能從已知的點(diǎn)數(shù)或花色中推知這張牌是什么牌嗎?于是,老師聽到了如下的對話:學(xué)生甲:我不知道這張牌;學(xué)生乙:我知道你不知道這張牌;學(xué)生甲:現(xiàn)在我知道這張牌了;學(xué)生乙:我也知道了.則這張牌是( )
A. 草花5B. 紅桃![]()
C. 紅桃4D. 方塊5
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為常數(shù).
為常數(shù).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() 有兩個相異零點(diǎn)
有兩個相異零點(diǎn)![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若數(shù)列![]() 、
、![]() 滿足
滿足![]() (
(![]() N*),則稱
N*),則稱![]() 為數(shù)列
為數(shù)列![]() 的“偏差數(shù)列”.
的“偏差數(shù)列”.
(1)若![]() 為常數(shù)列,且為
為常數(shù)列,且為![]() 的“偏差數(shù)列”,試判斷
的“偏差數(shù)列”,試判斷![]() 是否一定為等差數(shù)列,并說明理由;
是否一定為等差數(shù)列,并說明理由;
(2)若無窮數(shù)列![]() 是各項均為正整數(shù)的等比數(shù)列,且
是各項均為正整數(shù)的等比數(shù)列,且![]() ,
,![]() 為數(shù)列
為數(shù)列![]() 的“偏差數(shù)列”,求
的“偏差數(shù)列”,求![]() 的值;
的值;
(3)設(shè)![]() ,
,![]() 為數(shù)列
為數(shù)列![]() 的“偏差數(shù)列”,
的“偏差數(shù)列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 對任意
對任意![]() 恒成立,求實數(shù)M的最小值.
恒成立,求實數(shù)M的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,點(diǎn)
中,點(diǎn)![]() ,
,![]() ,
,![]() ,對角線
,對角線![]() ,
,![]() 交于點(diǎn)P.
交于點(diǎn)P.
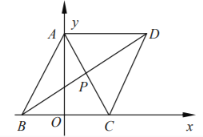
(1)求直線![]() 的方程;
的方程;
(2)若點(diǎn)E,F分別在平行四邊形![]() 的邊
的邊![]() 和
和![]() 上運(yùn)動,且
上運(yùn)動,且![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)試寫出三角形![]() 區(qū)域(包括邊界)所滿足的線性約束條件,若在該區(qū)域上任取一點(diǎn)M,使
區(qū)域(包括邊界)所滿足的線性約束條件,若在該區(qū)域上任取一點(diǎn)M,使![]() ,試求
,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com