Question

不等式4^x+a•2^x+1≥0對一切x∈R恒成立，則a的取值范圍是     ．

Answer 1

【答案】分析：4^x+a•2^x+1≥0對一切x∈R恒成立轉化為t²+at+1≥0對一切t＞0恒成立，再利用開口向上的二次函數在固定區間上最值的求法，求出a的取值范圍，
解答：解；令t=2^x 則t＞0，f（t）=t²+at+1，對稱軸為t=-，
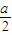
原不等式轉化為t²+at+1≥0對一切t＞0恒成立，
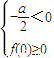
須有或⇒a＞0或a=0，∴a≥0
故答案為 a≥0．
點評：本題考查了函數問題中的恒成立問題，在解題過程中用到了轉化的數學思想，是基礎題．