補集是以“全集”為前提而建立的概念，而全集又是相對于所研究的問題而言的一個概念；只要包含研究問題的全體元素的集合都可作為________．
科目：高中數學 來源： 題型：
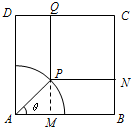如圖邊長為2的正方形花園的一角是以A為中心，1為半徑的扇形水池．現需在其余部分設計一個矩形草坪PNCQ，其中P是水池邊上任意一點，點N、Q分別在邊BC和CD上，設∠PAB為θ．| PN | PM |
查看答案和解析>>
科目：高中數學 來源： 題型：
| 12 |
| 5 |
| Tn+1 |
| Tn |
| 11 |
| 3 |
查看答案和解析>>
科目：高中數學 來源： 題型：
查看答案和解析>>
科目：高中數學 來源：2011-2012學年山東省菏澤市高三5月高考沖刺題理科數學試卷（解析版） 題型：解答題
已知函數
的圖象過坐標原點O,且在點
處的切線的斜率是
.
（Ⅰ）求實數
的值；
（Ⅱ）求
在區間
上的最大值；
（Ⅲ）對任意給定的正實數
，曲線
上是否存在兩點P、Q，使得
是以O為直角頂點的直角三角形，且此三角形斜邊中點在
軸上？說明理由.
【解析】第一問當
時，
，則
。
依題意得：
，即
解得
第二問當
時，
，令
得
，結合導數和函數之間的關系得到單調性的判定，得到極值和最值
第三問假設曲線上存在兩點P、Q滿足題設要求，則點P、Q只能在軸兩側。
不妨設
，則
，顯然
∵是以O為直角頂點的直角三角形，∴
即
（*）若方程（*）有解，存在滿足題設要求的兩點P、Q；
若方程（*）無解，不存在滿足題設要求的兩點P、Q.
（Ⅰ）當時，，則。
依題意得：，即 解得
（Ⅱ）由（Ⅰ）知，
①當時，，令得
當
變化時，
的變化情況如下表：
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調遞增 |
極大值 |
|
又
，
，
。∴在
上的最大值為2.
②當
時, 
.當
時, 
,最大值為0；
當
時, 在
上單調遞增。∴在最大值為
。
綜上，當
時，即
時，在區間上的最大值為2；
當
時，即
時，在區間上的最大值為。
（Ⅲ）假設曲線上存在兩點P、Q滿足題設要求，則點P、Q只能在軸兩側。
不妨設，則，顯然
∵是以O為直角頂點的直角三角形，∴
即 （*）若方程（*）有解，存在滿足題設要求的兩點P、Q；
若方程（*）無解，不存在滿足題設要求的兩點P、Q.
若
，則
代入（*）式得：
即
，而此方程無解，因此
。此時
，
代入（*）式得： 
即
（**）
令
，則
∴
在
上單調遞增， ∵ ∴
,∴
的取值范圍是
。
∴對于，方程（**）總有解，即方程（*）總有解。
因此，對任意給定的正實數，曲線上存在兩點P、Q，使得是以O為直角頂點的直角三角形，且此三角形斜邊中點在軸上
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
單調遞減