
���}Ŀ����֪![]() ��
��![]() �ǙE�A
�ǙE�A![]() ��
��![]() �ϵă��c(di��n)������
�ϵă��c(di��n)������![]() �����c(di��n)��ֱ��
�����c(di��n)��ֱ��![]() ��.
��.
��1����(d��ng)ֱ��![]() ��б��
��б��![]() ���ڕr(sh��)����(sh��)��(sh��)
���ڕr(sh��)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��2���O(sh��)![]() �ǙE�A
�ǙE�A![]() �����c(di��n)�����E�A
�����c(di��n)�����E�A![]() �ϴ���һ�c(di��n)
�ϴ���һ�c(di��n)![]() ��ʹ
��ʹ![]() ����
����![]() ��ֵ.
��ֵ.
���𰸡���1��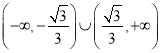 ����2��
����2��![]()
��������
��1���O(sh��)���c(di��n)![]() �������c(di��n)���
�������c(di��n)���![]() �����c(di��n)�ڙE�A��(n��i)����
�����c(di��n)�ڙE�A��(n��i)����![]() ���������k�ķ���
���������k�ķ���
��2����������(bi��o)����![]() ��
��![]() �����L(zh��ng)��ʽ��
�����L(zh��ng)��ʽ��![]() ���c(di��n)
���c(di��n)![]() �ڙE�A�ϣ���
�ڙE�A�ϣ���![]() ���M(j��n)����AB���̣��c�E�A(li��n)����
���M(j��n)����AB���̣��c�E�A(li��n)����![]() ���t����
���t����![]()
��1���O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]() ��
��
��ʽ���p�ã�![]()
![]() ��
��
�ɾ���![]() �����c(di��n)��ֱ��
�����c(di��n)��ֱ��![]() �ϣ����O(sh��)�����c(di��n)
�ϣ����O(sh��)�����c(di��n)![]() ����?y��n)�ֱ��
����?y��n)�ֱ��![]() ��б�ʴ��ڣ�����
��б�ʴ��ڣ�����![]() ��
��
�O(sh��)��б�ʞ�![]() ����
����![]() ʽ��
ʽ��![]() ����
����![]() .
.
������![]() �����c(di��n)
�����c(di��n)![]() ���ڙE�A��(n��i)�����t
���ڙE�A��(n��i)�����t![]() �����
�����![]() .
.
��![]() �������
������б��![]() ��ȡֵ������
��ȡֵ������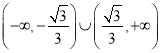 .
.
��2���ɣ�1��֪![]() ��
��![]() ����?y��n)�E�A�����c(di��n)
����?y��n)�E�A�����c(di��n)![]() ��
��![]() ��
��
����![]() ��
��![]() ���O(sh��)
���O(sh��)![]() ���t
���t![]() ��
��
![]()
![]() ��
��![]() ��
��
![]() ��
��
ͬ���ɵ�![]() ����?y��n)��c(di��n)
����?y��n)��c(di��n)![]() �ڙE�A�ϣ�����
�ڙE�A�ϣ�����![]() ��
��
���![]() .��(d��ng)
.��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��ֱ��
��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
����![]() ��
��![]() ���ɸ��cϵ��(sh��)�P(gu��n)ϵ��
���ɸ��cϵ��(sh��)�P(gu��n)ϵ��![]() .
.
�t![]()
![]() .
.
�Ɍ�(du��)�Q��֪����(d��ng)![]() �r(sh��)
�r(sh��)![]() Ҳ������
Ҳ������![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() �����ֵ��3,��D�������ɗl��(du��)�Q�S֮�g�ľ��x��
�����ֵ��3,��D�������ɗl��(du��)�Q�S֮�g�ľ��x��![]() .
.
(��)��(sh��)![]() �Ľ���ʽ�ͮ�(d��ng)
�Ľ���ʽ�ͮ�(d��ng)![]() �r(sh��)
�r(sh��)![]() ���{(di��o)�p�^(q��)�g��
���{(di��o)�p�^(q��)�g��
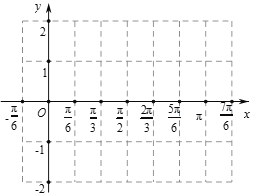
(��)![]() �ĈD������ƽ���Ƅ�(d��ng)
�ĈD������ƽ���Ƅ�(d��ng)![]() ��(g��)�L(zh��ng)�Ȇ�λ,������ƽ��1��(g��)�L(zh��ng)�Ȇ�λ,�õ�
��(g��)�L(zh��ng)�Ȇ�λ,������ƽ��1��(g��)�L(zh��ng)�Ȇ�λ,�õ�![]() �ĈD��,�á����c(di��n)��������
�ĈD��,�á����c(di��n)��������![]() ��
��![]() ��(n��i)�Ĵ��D��.
��(n��i)�Ĵ��D��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D�����������F![]() �У�
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
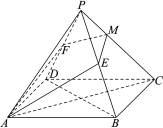
��1�����������F![]() ��ȫ��e��
��ȫ��e��
��2����ƽ��![]() �c��
�c��![]() �����c(di��n)
�����c(di��n)![]() ����ƽ��
����ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵĴ�С���÷����Ǻ���(sh��)ֵ��ʾ����
�����J����ǵĴ�С���÷����Ǻ���(sh��)ֵ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���x��R�ϵĺ���(sh��)![]() ��[0��7]����1��6�ɂ�(g��)���c(di��n)���Һ���(sh��)
��[0��7]����1��6�ɂ�(g��)���c(di��n)���Һ���(sh��)![]() �c����(sh��)
�c����(sh��)![]() ����ż����(sh��)���t
����ż����(sh��)���t![]() ��[0��2019]�ϵ����c(di��n)�����У� ����(g��)
��[0��2019]�ϵ����c(di��n)�����У� ����(g��)
A.404B.406C.808D.812
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�{(di��o)��C(j��)��(g��u)���˽��˂�ij��(g��)�a(ch��n)Ʒ��ʹ����r�Ƿ��c�Ԅe���P(gu��n)���ھW(w��ng)���M(j��n)���ˆ����{(di��o)�飬���{(di��o)��Y(ji��)�����S�C(j��)��ȡ��50���M(j��n)�нy(t��ng)Ӌ(j��)���õ�����![]() ��(li��n)����
��(li��n)����
���� | Ů�� | ��Ӌ(j��) | |
ʹ�� | 15 | 5 | 20 |
��ʹ�� | 10 | 20 | 30 |
��Ӌ(j��) | 25 | 25 | 50 |
��1��Ո(q��ng)����(j��)�{(di��o)��Y(ji��)���֢��������ж������J(r��n)��ʹ��ԓ�a(ch��n)Ʒ�c�Ԅe���P(gu��n)��
��2���ڲ�ʹ��ԓ�a(ch��n)Ʒ�����У����Ԅe�÷ӳ�ӳ�ȡ6�ˣ���?g��u)��@6�����S�C(j��)��ȡ2�˅���ij�(xi��ng)���(d��ng)�����@2����ǡ��һλŮ�Եĸ���.
����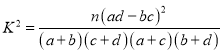
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��{an}��ǰn�(xi��ng)��Sn��2an��1��
��1����(sh��)��{an}��ͨ�(xi��ng)��ʽ��
��2������(sh��)��{bn}�M��bn��anlog2an+1����(sh��)��{bn}��ǰn�(xi��ng)��Tn��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪ ������������(g��)��ͬ��(sh��)��(sh��)
������������(g��)��ͬ��(sh��)��(sh��)![]() ʹ��
ʹ��![]() ���t
���t![]() ��ȡֵ�����ǣ� ��
��ȡֵ�����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.��0��1��
D.��0��1��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ƽ����߅��![]() �У�
�У�![]() ,
,![]() ,
,![]() ,
,![]() ����������
����������![]() ��
��![]() ���۵�������
���۵�������![]() ��λ����ƽ��
��λ����ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ���c(di��n).
���c(di��n).
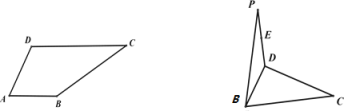
�������C��![]() ��
��
������ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���Aб�Ǟ�60����ֱ���c�E�A�քe����A��B���c(di��n)��
���Aб�Ǟ�60����ֱ���c�E�A�քe����A��B���c(di��n)��![]() ���c(di��n)C�ǙE�A�ϲ�ͬ��A��Bһ�c(di��n)���t��ABC��e�����ֵ��_____��
���c(di��n)C�ǙE�A�ϲ�ͬ��A��Bһ�c(di��n)���t��ABC��e�����ֵ��_____��
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com