
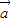 =(1,1,0),
=(1,1,0),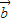 =(-1,0,2),且
=(-1,0,2),且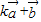 與
與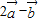 互相垂直,則k的值是( )
互相垂直,則k的值是( )


 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案科目:高中數學 來源: 題型:
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| n |
| n |
| a |
| b |
| π |
| 3 |
| x |
| 2 |
| a |
| n |
| m |
| n |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| a |
| 3 |
| 4 |
| a |
| b |
| b |
| b |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| 2 |
| 3 |
| b |
| p |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| π |
| 2 |
| 1 |
| 5 |
| sin2α-2sin2α |
| 1-tanα |
查看答案和解析>>
科目:高中數學 來源:設計選修數學2-1蘇教版 蘇教版 題型:013
已知向量a=(1,1,0),b=(-1,0,2)且ka+b與2a-b互相垂直,則k的值是
1
![]()
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分)已知向量a=(1,1),b=(1,0),c滿足a·c=0且|a|=|c|,b·c>0.
(1)求向量c;(2)若映射f:(x,y)→(x1,y1)=xa+yc,求映射f下(1,2)的原象.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com