
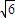 .
.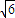 ,轉化為雙曲線與半徑為
,轉化為雙曲線與半徑為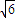 的圓A相切,聯立消去y得,利用△=0即可求得雙曲線的方程.
的圓A相切,聯立消去y得,利用△=0即可求得雙曲線的方程.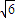 ,
,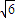 的圓A相切,
的圓A相切,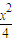 =1.
=1.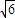 ,0)漸近線為x±2y=0,雙曲線方程為:
,0)漸近線為x±2y=0,雙曲線方程為: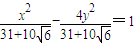 .
.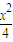 =1,
=1,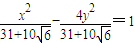 .
.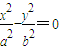 即可,反之,如此題設雙曲線方程為x2-4y2=m,避免了討論,條件(2)的設置增加了題目的難度,體現了轉化的思想,屬中檔題.
即可,反之,如此題設雙曲線方程為x2-4y2=m,避免了討論,條件(2)的設置增加了題目的難度,體現了轉化的思想,屬中檔題. 

 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 3 |
| π |
| 3 |
| 3 |
| 1 |
| 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com