
【題目】已知函數f(x)=(-x2+x-1)ex,其中e是自然對數的底數.
(1)求曲線f(x)在點(1,f(1))處的切線;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3個不同的根,求實數m的取值范圍.
x2+m有3個不同的根,求實數m的取值范圍.
【答案】見解析
【解析】(1)因為f(x)=(-x2+x-1)ex,
所以f′(x)=(-2x+1)ex+(-x2+x-1)ex=(-x2-x)ex.
所以曲線f(x)在點(1,f(1))處的切線斜率為
k=f′(1)=-2e.
又f(1)=-e,
所以所求切線方程為y+e=-2e(x-1),即2ex+y-e=0.
(2)因為f′(x)=(-2x+1)ex+(-x2+x-1)ex=(-x2-x)ex,
當x<-1或x>0時,f′(x)<0;
當-1<x<0時,f′(x)>0,
所以f(x)=(-x2+x-1)ex在(-∞,-1)上單調遞減,在(-1,0)上單調遞增,在(0,+∞)上單調遞減,
所以f(x)在x=-1處取得極小值f(-1)=-![]() ,在x=0處取得極大值f(0)=-1.
,在x=0處取得極大值f(0)=-1.
令g(x)=![]() x3+
x3+![]() x2+m,得g′(x)=x2+x.
x2+m,得g′(x)=x2+x.
當x<-1或x>0時,g′(x)>0;
當-1<x<0時,g′(x)<0,
所以g(x)在(-∞,-1)上單調遞增,在(-1,0)上單調遞減,在(0,+∞)上單調遞增.
故g(x)在x=-1處取得極大值g(-1)=![]() +m,在x=0處取得極小值g(0)=m.
+m,在x=0處取得極小值g(0)=m.
因為方程f(x)=![]() x3+
x3+![]() x2+m有3個不同的根,
x2+m有3個不同的根,
即函數f(x)與g(x)的圖象有3個不同的交點,
所以![]() ,即
,即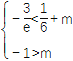 .
.
所以-![]() -
-![]() <m<-1.
<m<-1.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
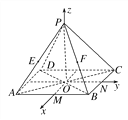
【題目】如圖,正四棱錐P-ABCD中,底面邊長為2,側棱長為![]() ,M,N分別為AB,BC的中點,以O為原點,射線OM,ON,OP分別為x軸、y軸、z軸的正方向建立空間直角坐標系.若E,F分別為PA,PB的中點,求A,B,C,D,E,F的坐標.
,M,N分別為AB,BC的中點,以O為原點,射線OM,ON,OP分別為x軸、y軸、z軸的正方向建立空間直角坐標系.若E,F分別為PA,PB的中點,求A,B,C,D,E,F的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若有窮數列![]() (
(![]() 是正整數),滿足
是正整數),滿足![]() 即
即![]() (
(![]() 是正整數,且
是正整數,且![]() ),就稱該數列為“對稱數列”。例如,數列
),就稱該數列為“對稱數列”。例如,數列![]() 與數列
與數列![]() 都是“對稱數列”.
都是“對稱數列”.
(1)已知數列![]() 是項數為9的對稱數列,且
是項數為9的對稱數列,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列, ![]() ,
, ![]() ,試求
,試求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并求前9項和
,并求前9項和![]() .
.
(2)若![]() 是項數為
是項數為![]() 的對稱數列,且
的對稱數列,且![]() 構成首項為31,公差為
構成首項為31,公差為![]() 的等差數列,數列
的等差數列,數列![]() 前
前![]() 項和為
項和為![]() ,則當
,則當![]() 為何值時,
為何值時, ![]() 取到最大值?最大值為多少?
取到最大值?最大值為多少?
(3)設![]() 是
是![]() 項的“對稱數列”,其中
項的“對稱數列”,其中![]() 是首項為1,公比為2的等比數列.求
是首項為1,公比為2的等比數列.求![]() 前
前![]() 項的和
項的和![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(λx+1)ln x-x+1.
(1)若λ=0,求f(x)的最大值;
(2)若曲線y=f(x)在點(1,f(1))處的切線與直線x+y+1=0垂直,證明:![]() >0.
>0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在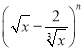 的展開式中,第5項的系數與第3項的系數之比是56:3.
的展開式中,第5項的系數與第3項的系數之比是56:3.
(1)求展開式中的所有有理項;
(2)求展開式中系數絕對值最大的項.
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lg(ax-bx),(a>1>b>0).
(1)求f(x)的定義域;
(2)若f(x)在(1,+∞)上遞增且恒取正值,求a,b滿足的關系式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017長沙模擬】如圖,在直棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=![]() ,AA1=3,D是BC的中點,點E在棱BB1上運動.
,AA1=3,D是BC的中點,點E在棱BB1上運動.
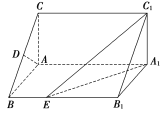
(1)求證:AD⊥C1E;
(2)當異面直線AC,C1E所成的角為60°時,求三棱錐C1A1B1E的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
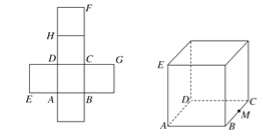
【題目】【2017銀川一中高考模擬文】一個正方體的平面展開圖及該正方體直觀圖的示意圖如圖所示,在正方體中,設BC的中點為M,GH的中點為N。
(1)請將字母F,G,H標記在正方體相應的頂點處(不需說明理由);
(2)證明:直線MN∥平面BDH;
(3)過點M,N,H的平面將正方體分割為兩部分,求這兩部分的體積比.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com