
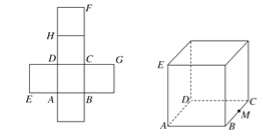
【題目】【2017銀川一中高考模擬文】一個正方體的平面展開圖及該正方體直觀圖的示意圖如圖所示,在正方體中,設BC的中點為M,GH的中點為N。
(1)請將字母F,G,H標記在正方體相應的頂點處(不需說明理由);
(2)證明:直線MN∥平面BDH;
(3)過點M,N,H的平面將正方體分割為兩部分,求這兩部分的體積比.
【答案】(1)詳見解析;(2)詳見解析. (3) 3∶1
【解析】 (1)點F,G,H的位置如圖所示.

(2)證明:連接BD,設O為BD的中點,連接OM,OH,AC,BH,MN。
∵M,N分別是BC,GH的中點,
∴OM∥CD,且OM=![]() CD,NH∥CD,且NH=
CD,NH∥CD,且NH=![]() CD,
CD,
∴OM∥NH,OM=NH,則四邊形MNHO是平行四邊形,∴MN∥OH,
又∵MN平面BDH,OH平面BDH,∴MN∥平面BDH。
(3)由(2)知OM∥NH,OM=NH,連接GM,MH,過點M,N,H的平面就是平面GMH,它將正方體分割為兩個同高的棱柱,高都是GH,底面分別是四邊形BMGF和三角形MGC,
體積比等于底面積之比,即3∶1。


科目:高中數學 來源: 題型:
【題目】【2017屆河北省衡水中學高三上學期六調】已知函數![]() ,其中
,其中![]() 均為實數,
均為實數,![]() 為自然對數的底數.
為自然對數的底數.
(1)求函數![]() 的極值;
的極值;
(2)設![]() ,若對任意的
,若對任意的![]() 恒成立,求實數
恒成立,求實數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(-x2+x-1)ex,其中e是自然對數的底數.
(1)求曲線f(x)在點(1,f(1))處的切線;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3個不同的根,求實數m的取值范圍.
x2+m有3個不同的根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017蘭州高考模擬】.在多面體ABCDEF中,底面ABCD是梯形,四邊形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
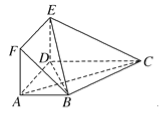
(1)求證:平面EBC⊥平面EBD;
(2)設M為線段EC上一點,且3EM=EC,試問在線段BC上是否存在一點T,使得MT∥平面BDE,若存在,試指出點T的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產電飯煲,每年需投入固定成本40萬元,每生產1萬件還需另投入16萬元的變動成本,設該公司一年內共生產電飯煲![]() 萬件并全部銷售完,每一萬件的銷售收入為
萬件并全部銷售完,每一萬件的銷售收入為![]() 萬元,且
萬元,且![]() (
(![]() ),該公司在電飯煲的生產中所獲年利潤為
),該公司在電飯煲的生產中所獲年利潤為![]() (萬元),(注:利潤=銷售收入-成本)
(萬元),(注:利潤=銷售收入-成本)
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (萬件)的函數解析式,并求年利潤的最大值;
(萬件)的函數解析式,并求年利潤的最大值;
(2)為了讓年利潤![]() 不低于2360萬元,求年產量
不低于2360萬元,求年產量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“開門大吉”是中央電視臺推出的娛樂節目.選手面對1~8號8扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌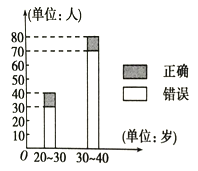
的名字,方可獲得該扇門對應的家庭夢想基金.在一次場外調查中,發現參賽選手多數分為兩個年齡段:20~30;30~40(單位:歲),其猜對歌曲名稱與否的人數如圖所示.
(1) 完成下列2×2列聯表(見答題紙);
(2)判斷是否有90%的把握認為猜對歌曲名稱與否和年齡有關;說明你的理由.(下面的臨界值表供參考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(參考公式: 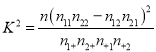 ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2-3x+2≤0},集合B={y|y=x2-2x+a},集合C={x|x2-ax-4≤0}.命題p:A∩B≠;命題q:AC.
(1)若命題p為假命題,求實數a的取值范圍;
(2)若命題p∧q為真命題,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究某學科成績(滿分100分)是否與學生性別有關,采用分層抽樣的方法,從高二年級抽取了30名男生和20名女生的該學科成績,得到下圖所示女生成績的莖葉圖.其中抽取的男生中有21人的成績在80分以下,規定80分以上為優秀(含80分).
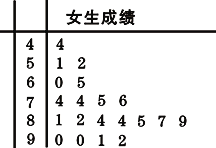
(1)請根據題意,將2×2列聯表補充完整;
優秀 | 非優秀 | 總計 | |
男生 | |||
女生 | |||
總計 | 50 |
(2)據此列聯表判斷,是否有90%的把握認為該學科成績與性別有關?
附: 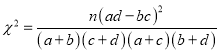 ,其中
,其中![]() .
.
參考數據 | 當 |
當 | |
當 | |
當 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com