
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,對于任意
,對于任意![]() 滿足
滿足![]() ,且
,且![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,其前
,其前![]() 項和為
項和為![]() .
.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)令![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:對于任意正整數
,求證:對于任意正整數![]() ,都有
,都有![]() ;
;
(3)將數列![]() 、
、![]() 的項按照“當
的項按照“當![]() 為奇數時,
為奇數時,![]() 放在前面”,“當
放在前面”,“當![]() 為偶數時,
為偶數時,![]() 放在前面”的要求進行“交叉排列”得到一個新的數列:
放在前面”的要求進行“交叉排列”得到一個新的數列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 求這個新數列的前
求這個新數列的前![]() 項和
項和![]() .
.
【答案】(1)![]() ,
,![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)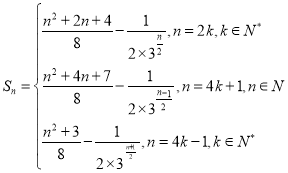 .
.
【解析】
(1)由題意可知數列![]() 為等差數列,確定該數列的首項和公差,可求出數列
為等差數列,確定該數列的首項和公差,可求出數列![]() 的通項公式,可求出
的通項公式,可求出![]() ,再由
,再由 可求出數列
可求出數列![]() 的通項公式,由等差中項法可知數列
的通項公式,由等差中項法可知數列![]() 為等差數列,從而可得出數列
為等差數列,從而可得出數列![]() 為等比數列,且設該等比數列的公比為
為等比數列,且設該等比數列的公比為![]() ,結合題中條件求出
,結合題中條件求出![]() 和
和![]() 的值,即可求出數列
的值,即可求出數列![]() 的通項公式;
的通項公式;
(2)利用錯位相減法求出數列![]() 的前
的前![]() 項和
項和![]() ,即可證明出
,即可證明出![]() ;
;
(3)求出數列![]() 的前
的前![]() 項和
項和![]() ,對
,對![]() 進行分類討論,利用等差數列和等比數列的求和公式可得出
進行分類討論,利用等差數列和等比數列的求和公式可得出![]() .
.
(1)![]() 且
且![]() ,所以,數列
,所以,數列![]() 是以
是以![]() 為首項,以
為首項,以![]() 為公差的等差數列,
為公差的等差數列,![]() ,
,![]() .
.
當![]() 時,
時,![]() .
.
![]() 也適合上式,所以,
也適合上式,所以,![]() .
.
![]() ,即
,即![]() ,
,
所以,數列![]() 為等差數列,設其公差為
為等差數列,設其公差為![]() ,則
,則![]() ,
,
![]() ,所以,數列
,所以,數列![]() 是正項等比數列,設其公比為
是正項等比數列,設其公比為![]() ,則
,則![]() .
.
由題意可得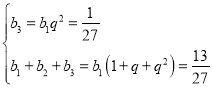 ,解得
,解得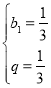 ,
,
因此,![]() ;
;
(2)![]() ,
,
![]() ,①
,①
則![]() ,②
,②
①![]() ②得
②得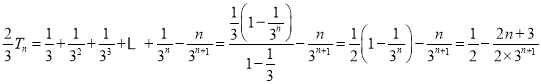 ,
,
化簡得![]() ;
;
(3)數列![]() 的前
的前![]() 項和為
項和為![]() ,
,
數列![]() 的前
的前![]() 項和為
項和為 ,
,
①當![]() 時,
時,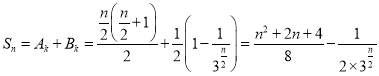 ;
;
②當![]() 時,
時,![]()
 ,
,
特別地,當![]() 時,
時,![]() 也適合上式;
也適合上式;
③當![]() 時,
時,![]()
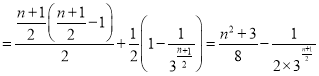 .
.
綜上所述,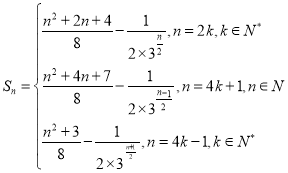 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,若在定義域內存在
,若在定義域內存在![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 為函數
為函數![]() 的局部對稱點.
的局部對稱點.
(1)若![]() 、
、![]() 且
且![]() ,證明:函數
,證明:函數![]() 必有局部對稱點;
必有局部對稱點;
(2)若函數![]() 在區間
在區間![]() 內有局部對稱點,求實數
內有局部對稱點,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 在
在![]() 上有局部對稱點,求實數
上有局部對稱點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知首項大于0的等差數列![]() 的公差
的公差![]() ,且
,且![]() ;
;
(1)求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 滿足:
滿足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;
;
①求數列![]() 的通項
的通項![]() ;
;
②是否存在實數![]() ,使得數列
,使得數列![]() 為等比數列?若存在,求出
為等比數列?若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為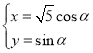 (其中
(其中![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 、
、![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() :
:![]() 與曲線
與曲線![]() ,
,![]() 分別交于點
分別交于點![]() ,
,![]() (且點
(且點![]() ,
,![]() 均異于原點
均異于原點![]() ),當
),當![]() 時,求
時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,某傳動裝置由兩個陀螺![]() ,
,![]() 組成,陀螺之間沒有滑動,每個陀螺都由具有公共軸的圓錐和圓柱兩個部分構成,每個圓柱的底面半徑和高都是相應圓錐底面半徑的
組成,陀螺之間沒有滑動,每個陀螺都由具有公共軸的圓錐和圓柱兩個部分構成,每個圓柱的底面半徑和高都是相應圓錐底面半徑的![]() ,且
,且![]() ,
,![]() 的軸相互垂直,它們相接觸的直線與
的軸相互垂直,它們相接觸的直線與![]() 的軸所成角
的軸所成角![]() ,若陀螺
,若陀螺![]() 中圓錐的底面半徑為
中圓錐的底面半徑為![]() (
(![]() );
);
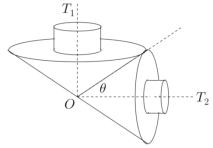
(1)求陀螺![]() 的體積;
的體積;
(2)當陀螺![]() 轉動一圈時,陀螺
轉動一圈時,陀螺![]() 中圓錐底面圓周上一點
中圓錐底面圓周上一點![]() 轉動到點
轉動到點![]() ,求
,求![]() 與
與![]() 之間的距離;
之間的距離;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() ,若
,若![]() (
(![]() 是與
是與![]() 無關的常數,
無關的常數,![]() )則稱數列
)則稱數列![]() 叫做“弱等差數列”已知數列
叫做“弱等差數列”已知數列![]() 滿足:
滿足:![]() 且
且![]() ,對于
,對于![]() 恒成立,(其中
恒成立,(其中![]() 都是常數)
都是常數)
(1)求證:數列![]() 是“弱等差數列”,并求出數列
是“弱等差數列”,并求出數列![]() 的通項公式
的通項公式
(2)當![]() 時,若數列
時,若數列![]() 是單調遞增數列,求
是單調遞增數列,求![]() 的取值范圍
的取值范圍
(3)若![]() ,且
,且![]() ,數列
,數列![]() 滿足:
滿足:![]() ,求
,求![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函數
),都在函數![]() (
(![]() ,
,![]() )的圖像上;
)的圖像上;
(1)若數列![]() 是等差數列,求證:數列
是等差數列,求證:數列![]() 是等比數列;
是等比數列;
(2)設![]() ,函數
,函數![]() 的反函數為
的反函數為![]() ,若函數
,若函數![]() 與函數
與函數![]() 的圖像有公共點
的圖像有公共點![]() ,求證:
,求證:![]() 在直線
在直線![]() 上;
上;
(3)設![]() ,
,![]() (
(![]() ),過點
),過點![]() 、
、![]() 的直線
的直線![]() 與兩坐標軸圍成的三角形面積為
與兩坐標軸圍成的三角形面積為![]() ,問:數列
,問:數列![]() 是否存在最大項?若存在,求出最大項的值,若不存在,請說明理由;
是否存在最大項?若存在,求出最大項的值,若不存在,請說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地區的“微信健步走”活動情況,現用分層抽樣的方法從中抽取老、中、青三個年齡段人員進行問卷調查.已知抽取的樣本同時滿足以下三個條件:
(i)老年人的人數多于中年人的人數;
(ii)中年人的人數多于青年人的人數;
(iii)青年人的人數的兩倍多于老年人的人數.
①若青年人的人數為4,則中年人的人數的最大值為___________.
②抽取的總人數的最小值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com