
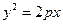 (
(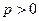 )的焦點(diǎn)為橢圓
)的焦點(diǎn)為橢圓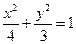 的右焦點(diǎn),點(diǎn)
的右焦點(diǎn),點(diǎn)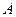 、
、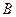 為拋物線上的兩點(diǎn),
為拋物線上的兩點(diǎn),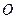 是拋物線的頂點(diǎn),
是拋物線的頂點(diǎn),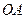 ⊥
⊥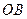 .
. 過定點(diǎn)
過定點(diǎn)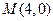 ;
; 的中點(diǎn)為
的中點(diǎn)為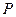 ,求點(diǎn)
,求點(diǎn)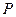 到直線
到直線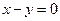 的距離的最小值.
的距離的最小值.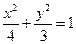 的右焦點(diǎn)
的右焦點(diǎn)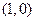 ,由題意知
,由題意知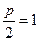 ∴
∴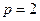 .……2分
.……2分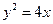 .……………………………………………………3分
.……………………………………………………3分
 方程為
方程為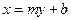 ,
,
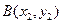 .
.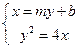 得
得 .…………………………………4分
.…………………………………4分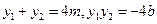 .…………………………………………………5分
.…………………………………………………5分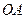 ⊥
⊥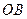 ,
,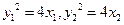 ,
, ,∴
,∴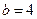 .……………………
.…………………… ……………7分
……………7分 的方程為
的方程為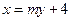 ,該直線恒過定點(diǎn)
,該直線恒過定點(diǎn)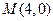 .……………………8分
.……………………8分 的斜率不存在時(shí),易求直線
的斜率不存在時(shí),易求直線 的方程為
的方程為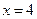 ,
, 過定點(diǎn)
過定點(diǎn)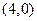 . ……………………………………………………………4分
. ……………………………………………………………4分 的斜率存在時(shí),設(shè)直線
的斜率存在時(shí),設(shè)直線 的方程為:
的方程為: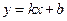
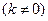 ,
,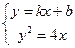 得
得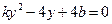 .
.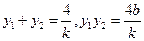 . ………………………………………………5分
. ………………………………………………5分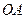 ⊥
⊥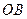 ,
,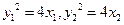 ,
,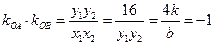 ,∴
,∴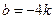 . ……………………………7分
. ……………………………7分 的方程為
的方程為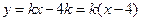 該直線恒過定點(diǎn)
該直線恒過定點(diǎn)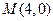 .……………8分
.……………8分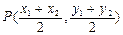 到直線
到直線
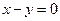 的距離:
的距離: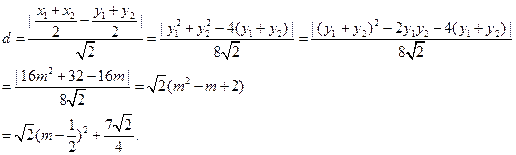 10分
10分
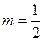 時(shí),
時(shí),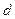 取最小值為
取最小值為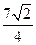 .……………………………………………12分
.……………………………………………12分

 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
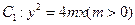 的準(zhǔn)線與
的準(zhǔn)線與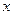 軸交于
軸交于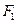 ,焦點(diǎn)為
,焦點(diǎn)為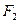 ;以
;以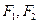 為焦點(diǎn),離心率
為焦點(diǎn),離心率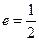 的橢圓
的橢圓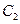 與拋物線
與拋物線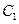 在
在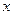 軸上方的交點(diǎn)為
軸上方的交點(diǎn)為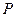 ,延長
,延長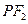 交拋物線于點(diǎn)
交拋物線于點(diǎn)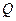 ,
,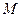 是拋物線
是拋物線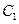 上一動(dòng)點(diǎn),且M在
上一動(dòng)點(diǎn),且M在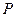 與
與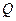 之間運(yùn)動(dòng).
之間運(yùn)動(dòng). 時(shí),求橢圓
時(shí),求橢圓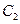 的方程;
的方程;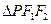 的邊長恰好是三個(gè)連續(xù)的自然數(shù)時(shí),求
的邊長恰好是三個(gè)連續(xù)的自然數(shù)時(shí),求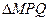 面積的最大值.
面積的最大值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
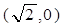 且與雙曲線
且與雙曲線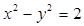 有且僅有一個(gè)公共點(diǎn),則這樣的直
有且僅有一個(gè)公共點(diǎn),則這樣的直| A.1 條 | B.2條 | C.3條 | D.4條 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
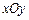 中,點(diǎn)P到兩
中,點(diǎn)P到兩 點(diǎn)
點(diǎn)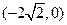 、
、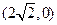 的距離之和等于6,設(shè)點(diǎn)P的軌跡為曲線
的距離之和等于6,設(shè)點(diǎn)P的軌跡為曲線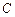 ,直線
,直線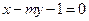 與曲線
與曲線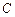 交于A、B兩點(diǎn).
交于A、B兩點(diǎn). 的方程;
的方程; 的值;
的值; 取何值時(shí),
取何值時(shí),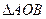 的面積最大,并求出面積的最大值.
的面積最大,并求出面積的最大值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
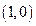 的距離比到直線
的距離比到直線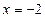 的距離少1,
的距離少1,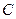 的軌跡的方程;
的軌跡的方程;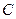 上異于原點(diǎn)
上異于原點(diǎn)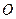 的兩個(gè)不同點(diǎn),直線
的兩個(gè)不同點(diǎn),直線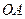 和
和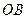 的傾
的傾 斜角分別為
斜角分別為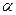 和
和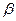 ,
, 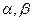 變化且
變化且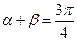 時(shí),證明直線
時(shí),證明直線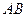 恒過定點(diǎn),并求出該定點(diǎn)的坐標(biāo).
恒過定點(diǎn),并求出該定點(diǎn)的坐標(biāo).查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
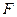 為拋物線
為拋物線 的焦點(diǎn),與拋物線相切于點(diǎn)
的焦點(diǎn),與拋物線相切于點(diǎn) 的直線
的直線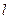 與
與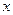 軸的交點(diǎn)為
軸的交點(diǎn)為 ,則
,則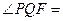 _________.
_________.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
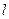 與拋物線
與拋物線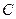 ,當(dāng)直線
,當(dāng)直線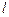 從
從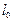 開始在平面上繞
開始在平面上繞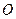 點(diǎn)按逆時(shí)針方向勻速旋轉(zhuǎn)(旋轉(zhuǎn)的角度不超過
點(diǎn)按逆時(shí)針方向勻速旋轉(zhuǎn)(旋轉(zhuǎn)的角度不超過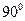 )時(shí),它掃過的面積
)時(shí),它掃過的面積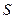 是時(shí)間
是時(shí)間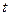 的函數(shù),則函數(shù)圖象大致是
的函數(shù),則函數(shù)圖象大致是
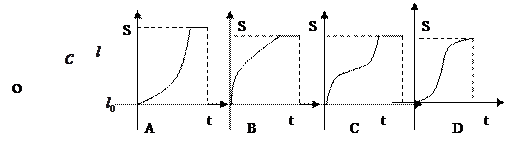
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
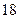 ,焦距為
,焦距為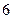 ,則橢圓的標(biāo)準(zhǔn)方程為
,則橢圓的標(biāo)準(zhǔn)方程為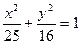 ;
;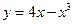 在點(diǎn)
在點(diǎn)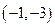 處的切線方程是
處的切線方程是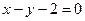 ;
;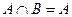 ,則
,則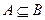 ”的逆否命題是:“若
”的逆否命題是:“若 ,則
,則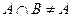 ”;
”;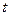 秒時(shí)距水面高度
秒時(shí)距水面高度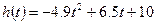 (單位:米),則該運(yùn)動(dòng)員的初速度為
(單位:米),則該運(yùn)動(dòng)員的初速度為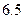 (米/秒);
(米/秒);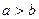 ”是“
”是“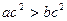 ”的充分條件。
”的充分條件。 查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com