新思維假期作業暑假吉林大學出版社系列答案
藍天教育暑假優化學習系列答案科目：高中數學 來源：成功之路·突破重點線·數學（學生用書） 題型：044
求下列函數的最小正周期
(1)y＝tan
－
；
(2)y＝2|sin(4x－
)|；
(3)y＝(asin＋cosx)2(a∈R)；
(4)y＝2cosxsin(x＋)－
sin2x＋sinxcosx
查看答案和解析>>
科目：高中數學 來源：新課程高中數學疑難全解 題型：044
求下列函數的最小正周期：
(1)y＝tan x－cot x：
(2)y＝2cos xsin(x＋
)－
sin2x＋sin xcos x；
(3)y＝
；
(4)y＝2|sin(4x－)|．
查看答案和解析>>
科目：高中數學 來源：高考總復習全解 數學 一輪復習·必修課程 （人教實驗版） B版 人教實驗版 B版 題型：044
求下列函數的周期：
(1)y＝sin x＋cos x；
(2)y＝sin(2x＋
)cos 2x；
(3)y＝cos24x；
(4)y＝tan x－cot x．
查看答案和解析>>
科目：高中數學 來源：2008年高考沖刺解答題突破、數學 題型：044
已知函數y＝f(x)對于任意
(k∈Z)，都有式子f(a－tanθ)＝cotθ－1成立(其中a為常數)．
(Ⅰ)求函數y＝f(x)的解析式；
(Ⅱ)利用函數y＝f(x)構造一個數列，方法如下：
對于給定的定義域中的x1，令x2＝f(x1)，x3＝f(x2)，…，xn＝f(xn－1)，…在上述構造過程中，如果xi(i＝1，2，3，…)在定義域中，那么構造數列的過程繼續下去；如果xi不在定義域中，那么構造數列的過程就停止．
(ⅰ)如果可以用上述方法構造出一個常數列，求a的取值范圍；
(ⅱ)是否存在一個實數a，使得取定義域中的任一值作為x1，都可用上述方法構造出一個無窮數列{xn}？若存在，求出a的值；若不存在，請說明理由；
(ⅲ)當a＝1時，若x1＝－1，求數列{xn}的通項公式．
查看答案和解析>>
科目：高中數學 來源：2012年人教A版高中數學必修四1.4三角函數的圖像與性質練習卷（四）（解析版） 題型：解答題
求下列函數的單調區間：
(1)y＝tan
； (2)y＝
tan2x＋1；
(3)y＝3tan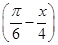
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
)的定義域、值域，并指出它的單調性．
