
分析 由已知中函數f(x)滿足f′(x)-f(x)=(1-2x)e-x,可得f(x)=xe-x,f′(x)=(1-x)e-x,逐一分析四個命題的真假,可得答案.
解答 解:①∵f′(x)-f(x)=(1-2x)e-x,
∴f(x)=xe-x,f′(x)=(1-x)e-x,
令f′(x)>0,解得:x<1,令f′(x)<0,解得:x>1,
∴函數f(x)在(-∞,1)遞增,在(1,+∞)遞減,
∴函數f(x)的極大值是f(1),沒有極小值;
故①正確;
②∵k=f′(x)=(1-x)e-x,
∴f″(x)=e-x(x-2),
令f″(x)>0,解得:x>2,令f″(x)<0,解得:x<2,
∴f′(x)在(-∞,2)遞減,在(2,+∞)遞增,
∴f′(x)最小值=f′(x)極小值=f′(2)=-$\frac{1}{{e}^{2}}$,
而x→∞時,f′(x)→0,
∴k的取值范圍是$-\frac{1}{e^2}<k<0$;
故②正確;
③結合①②函數f(x)在(2,+∞)上是凹函數,
∴$f({\frac{{{x_1}+{x_2}}}{2}})≤\frac{{f({x_1})+f({x_2})}}{2}$恒成立,
故③正確;
④當a≠b時,方程f(a)=f(b),不妨令a<b,
則a∈(0,1),
則ea∈(1,e),
又有ea為整數.
故ea=eb=2,
同理a>b時,也存在一對實數(a,b)使ea=eb=2,
故有兩對不同的實數解(a,b)滿足ea,eb均為整數.
故④正確;
故答案為:①②③④
點評 本題以命題的真假判斷與應用為載體,考查了導數的綜合應用,難度較大.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
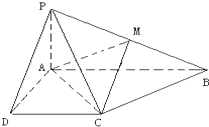 已知四棱錐P-ABCD的底面為直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中點.
已知四棱錐P-ABCD的底面為直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 分析法 | B. | 反證法 | C. | 綜合法 | D. | 間接證明法 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-1≤x≤4} | B. | {x|2<x≤3} | C. | {x|2≤x<3} | D. | {x|-1<x<4} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com