
分析 根據(jù)題意,分析可得a2-a+1=(a-$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,結(jié)合函數(shù)在[0,+∞)上是減函數(shù),可得f($\frac{3}{4}$)≤f(a2-a+1),又由函數(shù)為偶函數(shù),則有f(-$\frac{3}{4}$)=f($\frac{3}{4}$),綜合可得f(-$\frac{3}{4}$)≤f(a2-a+1),即可得答案.
解答 解:根據(jù)題意,a2-a+1=(a-$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,
由函數(shù)在[0,+∞)上是減函數(shù),則有f($\frac{3}{4}$)≥f(a2-a+1)
又由f(x)為R上的偶函數(shù),則f(-$\frac{3}{4}$)=f($\frac{3}{4}$)
則有f(-$\frac{3}{4}$)≥f(a2-a+1)
故答案為:≥.
點(diǎn)評 本題考查函數(shù)的奇偶性與單調(diào)性的綜合運(yùn)用,涉及代數(shù)式的大小比較,關(guān)鍵是比較(a2-a+1)的大小.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
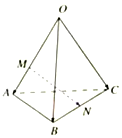 如圖,空間四邊形OABC中,點(diǎn)M、N分別OA、BC上,OM=2MA、BN=CN,則$\overrightarrow{MN}$=( )
如圖,空間四邊形OABC中,點(diǎn)M、N分別OA、BC上,OM=2MA、BN=CN,則$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 圓 | B. | 直線 | C. | 橢圓 | D. | 線段 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
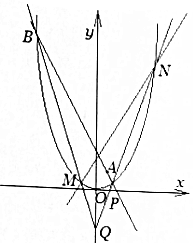 已知過點(diǎn)P($\frac{1}{2}$,0)的直線l與拋物線x2=y交于不同的兩點(diǎn)A,B,點(diǎn)Q(0,-1),連接AQ、BQ的直線與拋物線的另一交點(diǎn)分別為N,M,如圖所示.
已知過點(diǎn)P($\frac{1}{2}$,0)的直線l與拋物線x2=y交于不同的兩點(diǎn)A,B,點(diǎn)Q(0,-1),連接AQ、BQ的直線與拋物線的另一交點(diǎn)分別為N,M,如圖所示.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | ${x_2}{e^{x_1}}>{x_1}{e^{x_2}}$ | B. | ${x_2}{e^{x_1}}<{x_1}{e^{x_2}}$ | ||
| C. | lnx2-lnx1>2x2-2x1 | D. | lnx2-lnx1<2x2-2x1 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com