
【題目】已知函數![]() .
.
(1)求f[f(1)]的值;
(2)若f(x)>1,求x的取值范圍;
(3)判斷函數在(-2,+∞)上的單調性,并用定義加以證明.
【答案】(1)![]() (2)(-∞,-2) (3)增函數,證明見解析
(2)(-∞,-2) (3)增函數,證明見解析
【解析】
(1)可以求出![]() ,然后代入x=
,然后代入x=![]() 即可求出f[f(1)]的值;
即可求出f[f(1)]的值;
(2)根據f(x)>1即可得出![]() ,化簡然后解分式不等式即可;
,化簡然后解分式不等式即可;
(3)分離常數得出![]() ,從而可看出f(x)在(-2,+∞)上是增函數,根據增函數的定義證明:設任意的x1>x2>-2,然后作差,通分,得出
,從而可看出f(x)在(-2,+∞)上是增函數,根據增函數的定義證明:設任意的x1>x2>-2,然后作差,通分,得出![]() ,然后說明f(x1)>f(x2)即可得出f(x)在(-2,+∞)上是增函數.
,然后說明f(x1)>f(x2)即可得出f(x)在(-2,+∞)上是增函數.
(1)f[f(1)]=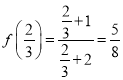 ;
;
(2)由f(x)>1得,![]() ,化簡得,
,化簡得,![]() ,
,
∴x<-2,
∴x的取值范圍為(-∞,-2);
(3)![]() ,f(x)在(-2,+∞)上是增函數,證明如下:
,f(x)在(-2,+∞)上是增函數,證明如下:
設x1>x2>-2,則:![]() =
=![]() ,
,
∵x1>x2>-2,
∴x1-x2>0,x1+2>0,x2+2>0,
∴![]() ,
,
∴f(x1)>f(x2),
∴f(x)在(-2,+∞)上是增函數.


 作業輔導系列答案
作業輔導系列答案科目:高中數學 來源: 題型:
【題目】隨著“北京八分鐘”在韓國平昌冬奧會驚艷亮相,冬奧會正式進入了北京周期,全社會對冬奧會的熱情空前高漲.
(1)為迎接冬奧會,某社區積極推動冬奧會項目在社區青少年中的普及,并統計了近五年來本社區冬奧項目青少年愛好者的人數![]() (單位:人)與時間
(單位:人)與時間![]() (單位:年),列表如下:
(單位:年),列表如下:

依據表格給出的數據,是否可用線性回歸模型擬合![]() 與
與![]() 的關系,請計算相關系數
的關系,請計算相關系數![]() 并加以說明(計算結果精確到0.01).
并加以說明(計算結果精確到0.01).
(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
附:相關系數公式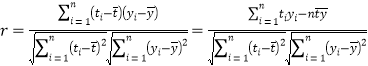 ,參考數據
,參考數據![]() .
.
(2)某冰雪運動用品專營店為吸引廣大冰雪愛好者,特推出兩種促銷方案.
方案一:每滿600元可減100元;
方案二:金額超過600元可抽獎三次,每次中獎的概率同為![]() ,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折. v
,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折. v
兩位顧客都購買了1050元的產品,并且都選擇第二種優惠方案,求至少有一名顧客比選擇方案一更優惠的概率;
②如果你打算購買1000元的冰雪運動用品,請從實際付款金額的數學期望的角度分析應該選擇哪種優惠方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市兩所高級中學聯合在暑假組織全體教師外出旅游,活動分為兩條線路:華東五市游和長白山之旅,且每位教師至多參加了其中的一條線路.在參加活動的教師中,高一教師占42.5%,高二教師占47.5%,高三教師占10%.參加華東五市游的教師占參加活動總人數的![]() ,且該組中,高一教師占50%,高二教師占40%,高三教師占10%.為了了解各條線路不同年級的教師對本次活動的滿意程度,現用分層隨機抽樣的方法從參加活動的全體教師中抽取一個容量為200的樣本.試確定:
,且該組中,高一教師占50%,高二教師占40%,高三教師占10%.為了了解各條線路不同年級的教師對本次活動的滿意程度,現用分層隨機抽樣的方法從參加活動的全體教師中抽取一個容量為200的樣本.試確定:
(1)參加長白山之旅的高一教師、高二教師、高三教師在該組分別所占的比例;
(2)參加長白山之旅的高一教師、高二教師、高三教師分別應抽取的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某聯歡晚會舉行抽獎活動,舉辦方設置了甲、乙兩種抽獎方案,方案甲的中獎率為![]() ,中獎可以獲得2分:方案乙的中獎率為
,中獎可以獲得2分:方案乙的中獎率為![]() ,中獎可以獲得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中獎與否互不影響,晚會結束后憑分數兌換獎品.
,中獎可以獲得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中獎與否互不影響,晚會結束后憑分數兌換獎品.
(1)若小明選擇方案甲抽獎,小紅選擇方案乙抽獎,記他們的累計得分為![]() ,求
,求![]() 的概率;
的概率;
(2)若小明、小紅兩人都選擇方案甲或都選擇方案乙進行抽獎,問:他們選擇何種方案抽獎,累計得分的均值較大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函數f(x)在R上單調遞增,求實數a的取值范圍;
(3)是否存在實數a,使不等式f(x)≥2x-3對任意x∈R恒成立?若存在,求出a的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() 滿足對于任意實數
滿足對于任意實數![]() ,
,![]() 都有
都有![]() ,且當
,且當![]() 時,
時,![]() ,
,![]() .
.
(1)判斷![]() 的奇偶性并證明;
的奇偶性并證明;
(2)判斷![]() 的單調性,并求當
的單調性,并求當![]() 時,
時,![]() 的最大值及最小值;
的最大值及最小值;
(3)解關于![]() 的不等式
的不等式![]()
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com