
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若不經過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,且直線
兩點,且直線![]() 與直線
與直線![]() 的斜率之和為
的斜率之和為![]() ,證明:直線
,證明:直線![]() 的斜率為定值.
的斜率為定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)由已知條件先求出橢圓![]() 的半焦距,再把
的半焦距,再把![]() 代入橢圓方程,結合性質
代入橢圓方程,結合性質![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可求出橢圓
,即可求出橢圓![]() 的方程;(2)設直線
的方程;(2)設直線![]() 的方程為
的方程為![]() 與橢圓的方程聯立,根據韋達定理及過兩點的斜率公式,利用直線
與橢圓的方程聯立,根據韋達定理及過兩點的斜率公式,利用直線![]() 的斜率之和為零可得
的斜率之和為零可得![]() ,從而可得結果.
,從而可得結果.
試題解析:(1)因為橢圓![]() 的焦距為
的焦距為![]() ,且過點
,且過點![]() ,所以
,所以![]() .因為
.因為![]() ,解得
,解得![]() ,所以橢圓
,所以橢圓![]() 的方程為
的方程為![]() .
.
(2)設點![]() ,則
,則![]() ,由
,由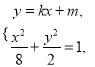 消去
消去![]() 得
得![]() ,(*)則
,(*)則![]() ,因為
,因為![]() ,即
,即![]() ,化簡得
,化簡得![]() .即
.即![]() .(**)代入得
.(**)代入得![]() ,整理得
,整理得![]() ,所以
,所以![]() 或
或![]() .若
.若![]() ,可得方程(*)的一個根為
,可得方程(*)的一個根為![]() ,不合題意,所以直線
,不合題意,所以直線![]() 的斜率為定值,該值為
的斜率為定值,該值為![]() .
.
【方法點晴】本題主要考查待定系數求橢圓方程以及直線與橢圓的位置關系和過兩點的斜率公式,屬于難題.用待定系數法求橢圓方程的一般步驟;①作判斷:根據條件判斷橢圓的焦點在![]() 軸上,還是在
軸上,還是在![]() 軸上,還是兩個坐標軸都有可能;②設方程:根據上述判斷設方程
軸上,還是兩個坐標軸都有可能;②設方程:根據上述判斷設方程![]() 或
或![]()
![]() ;③找關系:根據已知條件,建立關于
;③找關系:根據已知條件,建立關于![]() 、
、![]() 、
、![]() 的方程組;④得方程:解方程組,將解代入所設方程,即為所求.
的方程組;④得方程:解方程組,將解代入所設方程,即為所求.


科目:高中數學 來源: 題型:
【題目】某企業有兩個分廠生產某種零件,按規定內徑尺寸(單位:mm)的值落在[29.94,30.06)的零件為優質品.從兩個分廠生產的零件中各抽出了500件,量其內徑尺寸,得結果如下表:
甲廠:
分組 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
頻數 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙廠:
分組 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
頻數 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)試分別估計兩個分廠生產的零件的優質品率;
(2)由以上統計數據填下面![]() 列聯表,并問是否有
列聯表,并問是否有![]() 的把握認為“兩個分廠生產的零件的質量有差異”.
的把握認為“兩個分廠生產的零件的質量有差異”.
甲 廠 | 乙 廠 | 合計 | |
優質品 | |||
非優質品 | |||
合計 |
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在四棱錐S﹣ABCD中,底面ABCD是菱形,且∠BCD=60°,側面SAB是正三角形,且面SAB⊥面ABCD,F為SD的中點. 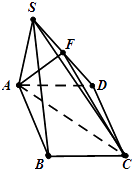
(1)證明:SB∥面ACF;
(2)求面SBC與面SAD所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)過點A(﹣
=1(a>b>0)過點A(﹣ ![]() ,
, ![]() ),離心率為
),離心率為 ![]() ,點F1 , F2分別為其左右焦點.
,點F1 , F2分別為其左右焦點.
(1)求橢圓C的標準方程;
(2)若y2=4x上存在兩個點M,N,橢圓上有兩個點P,Q滿足,M,N,F2三點共線,P,Q,F2三點共線,且PQ⊥MN.求四邊形PMQN面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)對任意的x,y∈R,總有f(x)+f(y)=f(x+y),且x<0時,f(x)>0.
(1)求證:函f(x)是奇函數;
(2)求證:函數f(x)是R上的減函數;
(3)若定義在(﹣2,2)上的函數f(x)滿足f(﹣m)+f(1﹣m)<0,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出三種函數模型:f(x)=xn(n>0),g(x)=ax(a>1)和h(x)=logax(a>1).根據它們增長的快慢,則一定存在正實數x0 , 當x>x0時,就有( )
A.f(x)>g(x)>h(x)
B.h(x)>g(x)>f(x)
C.f(x)>h(x)>g(x)
D.g(x)>f(x)>h(x)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉行“慶元旦”教工羽毛球單循環比賽(任意兩個參賽隊伍只比賽一場),有高一、高二、高三共三個隊參賽,高一勝高二的概率為![]() ,高一勝高三的概率為
,高一勝高三的概率為![]() ,高二勝高三的概率為
,高二勝高三的概率為![]() ,每場勝負相互獨立,勝者記1分,負者記0分,規定:積分相同時,高年級獲勝.
,每場勝負相互獨立,勝者記1分,負者記0分,規定:積分相同時,高年級獲勝.
(1)若高三獲得冠軍的概率為![]() ,求
,求![]() ;
;
(2)記高三的得分為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com