
【題目】函數f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3(ω>2)在一個周期內的圖象如圖所示,A為圖象的最高點,B,C為圖象與x軸的交點,且ABC為正三角形.
sinωx﹣3(ω>2)在一個周期內的圖象如圖所示,A為圖象的最高點,B,C為圖象與x軸的交點,且ABC為正三角形. 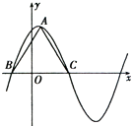
(1)求ω的值;
(2)求函數f(x)的值域.
【答案】
(1)解: ![]() =
= ![]()
∵正三角形的高為2 ![]() ,
,
∴BC=4,
∴函數f(x)的周期 ![]()
(2)解:函數f(x)=2 ![]() sin(
sin( ![]() x+
x+ ![]() ),
),
∵x∈R,
∴ ![]()
∴函數f(x)的值域為 ![]()
【解析】(1)利用兩角和公式和二倍角公式對函數解析式化簡,根據題意求得BC的長,進而求得三角函數的最下正周期,則ω可得.(2)根據(1)中求得f(x)的表達式,根據三角函數的性質求得函數的最大和最小值.
【考點精析】解答此題的關鍵在于理解函數y=Asin(ωx+φ)的圖象變換的相關知識,掌握圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2 ![]() sin
sin ![]() cos
cos ![]() ﹣2sin2
﹣2sin2 ![]() (ω>0)的最小正周期為3π.
(ω>0)的最小正周期為3π.
(I)求函數f(x)的單調遞增區間;
(Ⅱ)在△ABC中,a,b,c分別為角A,B,C所對的邊,a<b<c, ![]() a=2csinA,并且f(
a=2csinA,并且f( ![]() A+
A+ ![]() )=
)= ![]() ,求cosB的值.
,求cosB的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的右焦點為
的右焦點為![]() ,離心率為
,離心率為![]() ,過
,過![]() 作與
作與![]() 軸垂直的直線與橢圓交于
軸垂直的直線與橢圓交于![]() 兩點,
兩點,![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 的斜率存在且不為0,直線
的斜率存在且不為0,直線![]() 交橢圓于
交橢圓于![]() 兩點,若
兩點,若![]() 中點為
中點為![]() ,
,![]() 為原點,直線
為原點,直線![]() 交
交![]() 于點
于點![]() ,若以
,若以![]() 為直徑的圓過右焦點
為直徑的圓過右焦點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,公園有一塊邊長為2的等邊△ABC的邊角地,現修成草坪,圖中DE把草坪分成面積相等的兩部分,D在AB上,E在AC上.
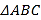
(1)設AD=x(x≥1),ED=y,求用x表示y的函數關系式;
(2)如果DE是灌溉水管,為節約成本,希望它最短,DE的位置應在哪里?如果DE是參觀線路,則希望它最長,DE的位置又應在哪里?請予證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信搶紅包”自2015年以來異常火爆,在某個微信群某次進行的搶紅包活動中,若所發紅包的總金額為9元,被隨機分配為1.49元,1.31元,2.19元,3.40元,0.61元,共5份,供甲、乙等5人搶,每人只能搶一次,則甲、乙二人搶到的金額之和不低于4元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() =1(a>b>0)的左、右焦點分別為F1,F2,P是橢圓上一點,|PF1|=λ|PF2|
=1(a>b>0)的左、右焦點分別為F1,F2,P是橢圓上一點,|PF1|=λ|PF2|![]() ,∠F1PF2=
,∠F1PF2=![]() ,則橢圓離心率的取值范圍為( )
,則橢圓離心率的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:x﹣y=1與圓M:x2+y2﹣2x+2y﹣1=0相交于A,C兩點,點B,D分別在圓M上運動,且位于直線AC兩側,則四邊形ABCD面積的最大值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com