
���}Ŀ����֪�E�A![]() ��
�� ![]() ������
������![]() ��
�� ![]() �����ҽ��c(di��n)�����x����
�����ҽ��c(di��n)�����x����![]() ��ֱ��
��ֱ��![]() �c�E�A���ڃɲ�ͬ�c(di��n)
�c�E�A���ڃɲ�ͬ�c(di��n)![]() ��
�� ![]() .��(d��ng)ֱ��
.��(d��ng)ֱ��![]() �^�E�A
�^�E�A![]() �ҽ��c(di��n)
�ҽ��c(di��n)![]() �҃Aб�Ǟ�
�҃Aб�Ǟ�![]() �r(sh��)��ԭ�c(di��n)
�r(sh��)��ԭ�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() .
.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395913728/STEM/2d7d70ba831f438cb4e191e234d85c18.png]
������E�A![]() �ķ��̣�
�ķ��̣�
������![]() ����(d��ng)
����(d��ng)![]() ��e��
��e��![]() �r(sh��)����
�r(sh��)����![]() �����ֵ.
�����ֵ.
���𰸡�(��) ![]() ��(��)5.
��(��)5.
��������ԇ�}���������������}������ǙE�A�Ę�(bi��o)��(zh��n)���̆��}������(j��)�}�O(sh��)�l���͙E�A�Ķ��x����������E�A![]() �ķ��̣�
�ķ��̣�
���������}������LjA�F�����е���ֵ�c�������}������ֱ�����̵�б�ʴ����c��δ֪����Ҫ��ֱ��б�ʴ��ںͲ����ڵăɷN��rӑՓ����(li��n)�����̽M�������f�_(d��)���������L(zh��ng)��ʽ���õ�![]() �������û�������ʽ�����������𰸡�
�������û�������ʽ�����������𰸡�
ԇ�}��������1����?y��n)�ֱ��![]() �ăAб�Ǟ�
�ăAб�Ǟ�![]() ��
�� ![]() �����ԣ�ֱ��
�����ԣ�ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
����֪��![]() ������
������![]() ����
����![]() ������
������![]() ��
�� ![]() ,
,
�E�A![]() �ķ���
�ķ���![]() ��
��
��2����(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)��
��б�ʲ����ڕr(sh��)�� ![]() ���c(di��n)�P(gu��n)��
���c(di��n)�P(gu��n)��![]() �S��(du��)�Q���t
�S��(du��)�Q���t![]() ��
��
��![]() �ڙE�A�ϣ��t
�ڙE�A�ϣ��t![]() ����
����![]() ���t
���t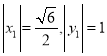
֪![]() =
=![]() ��
��
��(d��ng)ֱ��![]() ��б�ʴ��ڕr(sh��)���O(sh��)ֱ��
��б�ʴ��ڕr(sh��)���O(sh��)ֱ��![]() ��
��![]() ������
������![]() �ɵ�
�ɵ�
![]() ����
����![]() �����}��
�����}��![]() ����
����![]() ��
��
![]() ��
��
![]()
![]()
![]() ��
�� ![]() ,
,
����![]() ��
�� ![]() ��
��
��![]() ��
��
�t![]() ���M��
���M��![]() ,
,
��ǰ֪![]() ��
�� ![]() ��
��
![]() ��
��
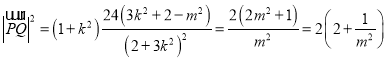
![]() ����(d��ng)�҃H��(d��ng)
����(d��ng)�҃H��(d��ng)![]() ����
����![]() �r(sh��)��̖(h��o)������
�r(sh��)��̖(h��o)������
��![]() ��
��
�C�Ͽ�֪![]() �����ֵ��
�����ֵ��![]() ��
��
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2015/12/14/1572357219860480/1572357226373120/EXPLANATION/e9a188fc269d42bdb85c3fefe32573fd.png]


 ��У�n��ϵ�д�
��У�n��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У���֪
�У���֪![]() ƽ��
ƽ��![]() ������߅��
������߅��![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ,
,![]() �քe��
�քe��![]() ,
,![]() �����c(di��n).
�����c(di��n).

��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2�����c(di��n)![]() ����
����![]() ��һ�c(di��n)����ƽ��
��һ�c(di��n)����ƽ��![]() ƽ��
ƽ��![]() �� ���C��
�� ���C��![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����![]() �У������Ҷ�����
�У������Ҷ�����![]() ��ֵ���@��(g��)��ֵ����
��ֵ���@��(g��)��ֵ����![]() ����ӈA��ֱ��
����ӈA��ֱ��![]() ��D2��ʾ��
��D2��ʾ��![]() �У���֪
�У���֪![]() ���c(di��n)M��ֱ��EF�Ϗ������\(y��n)��(d��ng)
���c(di��n)M��ֱ��EF�Ϗ������\(y��n)��(d��ng)![]() �c(di��n)M���cE��F�غ�
�c(di��n)M���cE��F�غ�![]() ����(du��)��M��ÿһ��(g��)λ�ã�ӛ
����(du��)��M��ÿһ��(g��)λ�ã�ӛ![]() ����ӈA��e�c
����ӈA��e�c![]() ����ӈA��e�ı�ֵ��
����ӈA��e�ı�ֵ��![]() ����ô
����ô![]() ����
����![]()

A. ![]() ��׃С��׃��
��׃С��׃��
B. �H��(d��ng)M�龀��EF�����c(di��n)�r(sh��)��![]() ȡ�����ֵ
ȡ�����ֵ
C. ![]() ��׃����׃С
��׃����׃С
D. ![]() ��һ��(g��)��ֵ
��һ��(g��)��ֵ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ij�y(c��)���ˆT���˜y(c��)�������������ܵ��_(d��)�ă��c(di��n)![]() ��
��![]() ֮�g�ľ��x�����������ϰ��ҵ�һ��(g��)�c(di��n)
֮�g�ľ��x�����������ϰ��ҵ�һ��(g��)�c(di��n)![]() ����
����![]() �c(di��n)�����^�쵽�c(di��n)
�c(di��n)�����^�쵽�c(di��n)![]() ��
��![]() ���ҵ�һ��(g��)�c(di��n)
���ҵ�һ��(g��)�c(di��n)![]() ����
����![]() �c(di��n)�����^�쵽�c(di��n)
�c(di��n)�����^�쵽�c(di��n)![]() ��
��![]() ���ҵ�һ��(g��)�c(di��n)
���ҵ�һ��(g��)�c(di��n)![]() ����
����![]() �c(di��n)�����^�쵽�c(di��n)
�c(di��n)�����^�쵽�c(di��n)![]() ��
��![]() �����y(c��)���õ���(sh��)��(j��)��
�����y(c��)���õ���(sh��)��(j��)��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ף�
���ף�

��1����![]() ����e��
����e��
��2����![]() ��
��![]() ֮�g�ľ��x��ƽ����
֮�g�ľ��x��ƽ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����һ�K�����ϷNֲһ�N���ÿ���Nֲ�ɱ���1000Ԫ����������Ј�(ch��ng)�r(ji��)����@�K���ϵĮa(ch��n)���������S�C(j��)�ԣ��һ���Ӱ푣�����w��r���±���
����a(ch��n)��(kg) | 300 | 500 |
���� | 0.5 | 0.5 |
�����Ј�(ch��ng)�r(ji��)��(Ԫ/kg) | 6 | 10 |
���� | 0.4 | 0.6 |
��1���O(sh��)X��ʾ���@�K���ϷNֲ1�������������(r��n)����X�ķֲ��У�
��2�������@�K�����B�m(x��)3���Nֲ��������@3����������2��������(r��n)������2000Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪a>0��b>0��a3��b3��2.�C����
(1)(a��b)(a5��b5)��4��
(2)a��b��2.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)F�钁�タC��x2��2py (p��0) �Ľ��c(di��n)���c(di��n)A(m��3)�ڒ��タC�ϣ���|AF|��5�����c(di��n)P�ǒ��タC�ϵ�һ��(g��)��(d��ng)�c(di��n)���O(sh��)�c(di��n)P��ֱ��![]() �ľ��x��
�ľ��x��![]() ���O(sh��)�c(di��n)P��ֱ��
���O(sh��)�c(di��n)P��ֱ��![]() �ľ��x��
�ľ��x��![]() ��
��
(1)���タC�ķ��̣�
(2) ��![]() ����Сֵ��
����Сֵ��
(3)��![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �ăɂ�(g��)���c(di��n)�քe��
�ăɂ�(g��)���c(di��n)�քe��![]() ��
��![]() ���x���ʞ�
���x���ʞ�![]() ���ҙE�A�Ă�(g��)��c(di��n)��(g��u)�ɵ�������e��
���ҙE�A�Ă�(g��)��c(di��n)��(g��u)�ɵ�������e��![]() ��
��
(1)��E�AC�ķ��̣�
(2)��ֱ��l ��y��x��m�c�E�AC����M��N���c(di��n)����MN���߅�����������Σ���c(di��n)��P(3����2)����m��ֵ����PMN����e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ���������
���������![]() �ķ�����
�ķ�����
��2����![]() ��
��![]() ̎���о���
̎���о���![]() ����
����![]() ��ֵ.���C����(d��ng)
��ֵ.���C����(d��ng)![]() )�r(sh��)��
)�r(sh��)�� ![]() .
.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com