
【題目】已知函數![]() .
.
(1)當![]() 時,探究
時,探究![]() 零點的個數;
零點的個數;
(2)①證明:![]() ;
;
②當![]() 時,證明:
時,證明:![]() .
.
【答案】(1)見解析;(2)①見證明;②見證明
【解析】
(1)利用導函數對a進行討論判斷即可.
(2)①對所證函數化簡,即證明![]() ,利用導函數研究其單調性,求解最值問題即可證明;②用(1)的結論,求出零點
,利用導函數研究其單調性,求解最值問題即可證明;②用(1)的結論,求出零點![]() ,得出單調性,計算最值
,得出單調性,計算最值![]() ,然后用
,然后用![]() 進行替換,然后用
進行替換,然后用![]() 去掉
去掉![]() ,轉化為關于
,轉化為關于![]() 的一次式,代入
的一次式,代入![]() 即可證明.
即可證明.
(1)解:![]() ,定義域為
,定義域為![]() .
.
二次函數![]() 的判別式為
的判別式為![]() ,對稱軸為
,對稱軸為![]() .
.
當![]() 時,二次函數
時,二次函數![]() 的圖像開口向下,判別式為
的圖像開口向下,判別式為![]() ,
,
所以![]() 在
在![]() 上有1個零點;
上有1個零點;
當![]() 時,
時,![]() 在
在![]() 上無零點;
上無零點;
當![]() 時,二次函數
時,二次函數![]() 的圖像開口向上,
的圖像開口向上,
①![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上無零點;
上無零點;
②![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上有1個零點
上有1個零點![]() ;
;
③![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上有2個不同的零點;
上有2個不同的零點;
綜上,當![]() 時,
時,![]() 在
在![]() 上無零點;
上無零點;
當![]() 時,
時,![]() 在
在![]() 上有1個零點;
上有1個零點;
當![]() 時,
時,![]() 在
在![]() 上有2個不同的零點;
上有2個不同的零點;
(2)①要證明:![]() ,只需要證明:
,只需要證明:![]() .
.
令![]() ,定義域為
,定義域為![]() ,
,![]() ,
,
所以![]() ,不難得到
,不難得到![]() 的最大值為
的最大值為![]() ,所以
,所以![]() 成立;
成立;
②由(1)得,當![]() 時,
時,![]() 在
在![]() 上有1個零點;設零點為
上有1個零點;設零點為![]() ,
,
則![]() ,解得,
,解得,![]() ,
,
進一步,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以![]()
![]() (※)
(※)
由(2)①得,
(※)![]()
![]()
![]() .
.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:
【題目】某校的1000名高三學生參加四門學科的選拔考試,每門試卷共有10道題,每題10分,規定:每門錯![]() 題成績記為
題成績記為![]() ,錯
,錯![]() 題成績記為
題成績記為![]() ,錯
,錯![]() 題成績記為
題成績記為![]() ,錯
,錯![]() 題成績記為
題成績記為![]() ,在錄取時,
,在錄取時,![]() 記為90分,
記為90分,![]() 記為80分,
記為80分,![]() 記為60分,
記為60分,![]() 記為50分.
記為50分.
根據模擬成績,每一門都有如下統計表:
答錯 題數 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
頻數 | 10 | 90 | 100 | 150 | 150 | 200 | 100 | 100 | 50 | 49 | 1 |
已知選拔性考試成績與模擬成績基本吻合.
(1)設![]() 為高三學生一門學科的得分,求
為高三學生一門學科的得分,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)預測考生4門總分為320概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
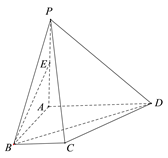
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(i)過點![]() 作一直線
作一直線![]() 與
與![]() 平行,在圖中畫出直線
平行,在圖中畫出直線![]() 并說明理由;
并說明理由;
(ii)求平面![]() 將三棱錐
將三棱錐![]() 分成的兩部分體積的比.
分成的兩部分體積的比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,且
為正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() ,
,![]() 的中點,動點
的中點,動點![]() 在線段
在線段![]() 上運動時,下列四個結論:①
上運動時,下列四個結論:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的為( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在R上的偶函數且以2為周期,則“
是定義在R上的偶函數且以2為周期,則“![]() 為
為![]() 上的增函數”是“
上的增函數”是“![]() 為
為![]() 上的減函數”的
上的減函數”的![]()
![]()
A. 充分而不必要的條件B. 必要而不充分的條件
C. 充要條件D. 既不充分也不必要的條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分) 已知雙曲線![]() 的兩個焦點為
的兩個焦點為![]() 的曲線C上.
的曲線C上.
(Ⅰ)求雙曲線C的方程;
(Ⅱ)記O為坐標原點,過點Q(0,2)的直線l與雙曲線C相交于不同的兩點E、F,若△OEF的面積為![]() 求直線l的方程
求直線l的方程
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com