【題目】已知
中，角
所對的邊分別是
，的面積為
，且
，
.
（1）求
的值；
（2）若
，求的值.
【答案】（1）
（2）
【解析】
（1）由已知利用三角形面積公式可得tanA＝2，利用同角三角函數基本關系式可求sinA，cosA，由三角形內角和定理，兩角和的余弦函數公式可求cosB的值．
（2）利用同角三角函數基本關系式可求sinB，利用正弦定理可得b的值，即可得S的值．
（1）∵S
bcsinA＝bccosA，
∴sinA＝2cosA，可得：tanA＝2，
∵△ABC中，A為銳角，
又∵sin2A+cos2A＝1，
∴可得：sinA
，cosA
，
又∵C
，
∴cosB＝﹣cos（A+C）＝﹣cosAcosC+sinAsinC
，
（2）在△ABC中，sinB
，
由正弦定理，可得：b
3，
∴S＝bccosA＝3．
輕松奪冠全能掌控卷系列答案科目：高中數學 來源： 題型：
【題目】運輸公司
年有
萬輛公交車，計劃
年投入
輛新型號公交車，以后每年投入的新型號公交車數量均比上年增加
.
（1）
年應投入多少輛新型號公交車？
（2）從年到年間共投入多少輛新型號公交車？
（3）從哪一年開始，該公司新型號公交車總量超過該公司公交車總量的
？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
（
）的離心率為
，橢圓
與
軸交于
兩點，且
．
（1）求橢圓的方程；
（2）設點
是橢圓上的一個動點，且點
在軸的右側，直線
與直線
交于
兩點，若以
為直徑的圓與
軸交于
，求點
橫坐標的取值范圍及
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
過點
，且右焦點為
．
（1）求橢圓
的方程；
（2）過點
的直線
與橢圓交于
兩點，交
軸于點
．若
，求證：
為定值；
（3）在（2）的條件下，若點不在橢圓的內部，點
是點關于原點
的對稱點，試求三角形
面積的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將
個不同的紅球和
個不同的白球，放入同一個袋中，現從中取出個球.
（1）若取出的紅球的個數不少于白球的個數，則有多少種不同的取法；
（2）取出一個紅球記
分，取出一個白球記
分，若取出個球的總分不少于
分，則有多少種不同的取法；
（3）若將取出的個球放入一箱子中，記“從箱子中任意取出個球，然后放回箱子中”為一次操作，如果操作三次，求恰有一次取到個紅球并且恰有一次取到個白球的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從甲、乙兩班各隨機抽取10名同學，下面的莖葉圖記錄了這20名同學在2018年高考語文作文題目中的成績（單位：分）.已知語文作文題目滿分為60分，“分數
分，為及格；分數
分，為高分”，若甲、乙兩班的成績的平均分都是44分，
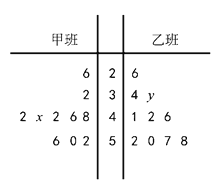
（1）求
的值；
（2）若分別從甲、乙兩班隨機各抽取1名成績為高分的學生，求抽到的學生中，甲班學生成績高于乙班學生成績的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
