
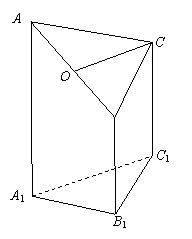
 右圖是一個直三棱柱(以
右圖是一個直三棱柱(以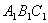 為底面)被
為底面)被
|
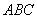 .
.
已知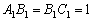 ,
, 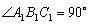 ,
,
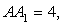
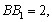
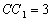 .
.
(Ⅰ)設點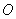 是
是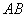 的中點,證明:
的中點,證明: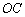 ∥平面
∥平面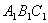 ;
;
(Ⅱ)求二面角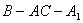 的大小.
的大小.
解:法一:
 (Ⅰ)證明:作
(Ⅰ)證明:作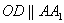 交
交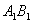 于
于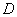 ,連
,連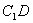 .……(1分)
.……(1分)
則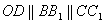 .
.
因為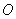 是
是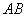 的中點,
的中點,
所以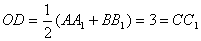 .
.
則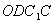 是平行四邊形,因此有
是平行四邊形,因此有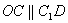 .……………………(3分)
.……………………(3分)
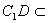 平面
平面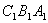 且
且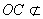 平面
平面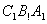 ,
,
則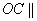 面
面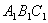 .
……………………(5分)
.
……………………(5分)
(Ⅱ)如圖,過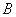 作截面
作截面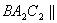 面
面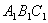 ,分別交
,分別交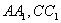 于
于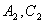 .
.
作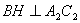 于
于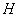 ,連
,連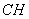 .
……………………(7分)
.
……………………(7分)
因為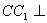 面
面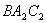 ,所以
,所以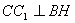 ,則
,則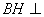 平面
平面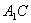 .
.
又因為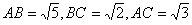
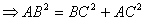 .
.
所以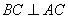 ,根據(jù)三垂線定理知
,根據(jù)三垂線定理知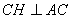 ,所以
,所以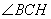 就是所求二面角的平面角.
就是所求二面角的平面角.
……………………(9分)
因為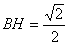 ,所以
,所以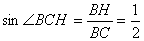 ,故
,故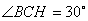 ,………(11分)
,………(11分)
即:所求二面角的大小為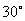 .
……………………(12分)
.
……………………(12分)
法二:
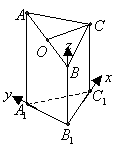 (Ⅰ)如圖,以
(Ⅰ)如圖,以 為原點建立空間直角坐標系, ………………(1分)
為原點建立空間直角坐標系, ………………(1分)
則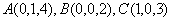
因為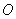 是
是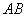 的中點,所以
的中點,所以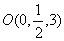 ,
,
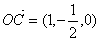 .
.
易知,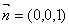 是平面
是平面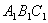 的一個法向量. ……(3分)
的一個法向量. ……(3分)
因為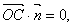
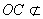 平面
平面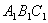 ,
,
所以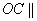 平面
平面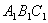 .
………………(5分)
.
………………(5分)
(Ⅱ)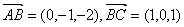 ,
,
設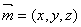 是平面
是平面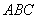 的一個法向量,則
的一個法向量,則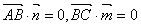 得:
得: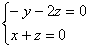
取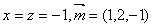 .
……………………(7分)
.
……………………(7分)
顯然,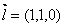 為平面
為平面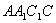 的一個法向量. ……………………(9分)
的一個法向量. ……………………(9分)
則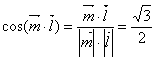 ,
……………………(11分)
,
……………………(11分)
結合圖形可知所求二面角為銳角.
所以二面角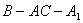 的大小是
的大小是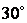 . ……………………(12分)
. ……………………(12分)


科目:高中數(shù)學 來源: 題型:
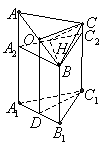
 右圖是一個直三棱柱(以A1B1C1為底面),被一平面所截得的幾何體,截面為ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3
右圖是一個直三棱柱(以A1B1C1為底面),被一平面所截得的幾何體,截面為ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 (本小題14分)右圖是一個直三棱柱(以
(本小題14分)右圖是一個直三棱柱(以![]() 為底面)
為底面)
被一平面所截得到的幾何體,截面為ABC.
已知![]() .
.
(1)設點O是AB的中點,證明:OC∥平面A1B1C1;
(2)證明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此幾何體的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 (本小題14分)右圖是一個直三棱柱(以
(本小題14分)右圖是一個直三棱柱(以![]() 為底面)
為底面)
被一平面所截得到的幾何體,截面為ABC.
已知![]() .
.
(1)設點O是AB的中點,證明:OC∥平面A1B1C1;
(2)證明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此幾何體的體積.
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆廣東汕頭金山中學高二上學期期中理科數(shù)學試卷(解析版) 題型:解答題
右圖是一個直三棱柱(以 為底面)被一平面所截得到的幾何體,截面為
為底面)被一平面所截得到的幾何體,截面為 .已知
.已知 ,
, ,
, ,
, ,
, .
.

(1)設點 是
是 的中點,證明:
的中點,證明: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
查看答案和解析>>
科目:高中數(shù)學 來源:2013屆遼寧省高三第四次階段測試理科數(shù)學試卷(解析版) 題型:解答題
(本小題滿分12分)右圖是一個直三棱柱(以 為底面)被一平面所截得到的幾何體,截面為
為底面)被一平面所截得到的幾何體,截面為 已知
已知 ,
, ,
, ,
, ,
,

(Ⅰ)設點 是
是 的中點,證明:
的中點,證明: 平面
平面 ;
;
(Ⅱ)求二面角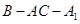 的大小;
的大小;
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com