
【題目】已知: ![]() =(2sinx,2cosx),
=(2sinx,2cosx), ![]() =(cosx,﹣cosx),f(x)=
=(cosx,﹣cosx),f(x)= ![]() .
.
(1)若 ![]() 與
與 ![]() 共線,且x∈(
共線,且x∈( ![]() ,π),求x的值;
,π),求x的值;
(2)求函數(shù)f(x)的周期;
(3)若對任意x∈[0, ![]() ]不等式m﹣2≤f(x)≤m+
]不等式m﹣2≤f(x)≤m+ ![]() 恒成立,求實數(shù)m的取值范圍.
恒成立,求實數(shù)m的取值范圍.
【答案】
(1)解:∵x∈( ![]() ,π),∴cosx≠0
,π),∴cosx≠0
又∵ ![]() 與
與 ![]() 共線∴
共線∴ ![]() =
= ![]() 即tanx=﹣1
即tanx=﹣1
∵x∈( ![]() ,π),∴x=
,π),∴x= ![]() =
= ![]()
(2)解:f(x)= ![]() =2sinxcosx﹣2cos2x=sin2x﹣cos2x﹣1
=2sinxcosx﹣2cos2x=sin2x﹣cos2x﹣1
= ![]() (sin2x
(sin2x ![]() ﹣cos2x
﹣cos2x ![]() )=
)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣1
)﹣1
故函數(shù)f(x)的周期T= ![]() =π
=π
(3)解:∵0 ![]()
∴ ![]() ≤
≤ ![]()
∴ ![]() ≤sin(2x﹣
≤sin(2x﹣ ![]() )≤1
)≤1
∴﹣2 ![]() ﹣1
﹣1 ![]() ,
,
即﹣2 ![]()
要使不等式m﹣2≤f(x) ![]() ,
,
對任意x ![]() ]上恒成立,
]上恒成立,
必須且只需 ![]() ,
,
即﹣1≤m≤0.
【解析】(1)運用共線的向量的性質(zhì)得出 ![]() =
= ![]() 即tanx=﹣1,結合x∈(
即tanx=﹣1,結合x∈( ![]() ,π),求解x的值.(2)化簡得出f(x)=
,π),求解x的值.(2)化簡得出f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )﹣1,根據(jù)三角函數(shù)的性質(zhì)得出周期,T═
)﹣1,根據(jù)三角函數(shù)的性質(zhì)得出周期,T═ ![]() (3)根據(jù)x的范圍得出
(3)根據(jù)x的范圍得出 ![]() ≤sin(2x﹣
≤sin(2x﹣ ![]() )≤1,確定﹣2
)≤1,確定﹣2 ![]() ,利用最大值,最小值問題求解得出只需
,利用最大值,最小值問題求解得出只需 ![]() 成立即可.
成立即可.


科目:高中數(shù)學 來源: 題型:
【題目】對于給定的正整數(shù)k,若數(shù)列{an}滿足![]()
=2kan對任意正整數(shù)n(n> k) 總成立,則稱數(shù)列{an} 是“P(k)數(shù)列”.
(1)證明:等差數(shù)列{an}是“P(3)數(shù)列”;
若數(shù)列{an}既是“P(2)數(shù)列”,又是“P(3)數(shù)列”,證明:{an}是等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
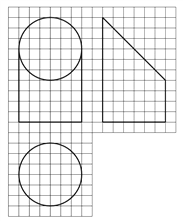
【題目】如圖,網(wǎng)格紙上小正方形的邊長為![]() ,粗實線畫出的是某幾何體的三視圖,該幾何體由一平面將一圓柱截去一部分所得,則該幾何體的體積為( )
,粗實線畫出的是某幾何體的三視圖,該幾何體由一平面將一圓柱截去一部分所得,則該幾何體的體積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在四棱錐![]() 中,
中, ![]() 為正三角形,平面
為正三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求三棱錐![]() 的體積;
的體積;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,請確定點
?若存在,請確定點![]() 的位置并證明;若不存在,說明理由.
的位置并證明;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線l經(jīng)過點(1,﹣2),且與直線m:4x﹣3y+1=0平行;
(1)求直線l的方程;
(2)求直線l被圓x2+y2=9所截得的弦長.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com