
【題目】已知直線x+y﹣1=0與橢圓 ![]() 相交于A,B兩點,線段AB中點M在直線
相交于A,B兩點,線段AB中點M在直線 ![]() 上.
上.
(1)求橢圓的離心率;
(2)若橢圓右焦點關于直線l的對稱點在單位圓x2+y2=1上,求橢圓的方程.
【答案】
(1)解:設A,B兩點的坐標分別為(x1,y1),(x2,y2),
由 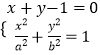 得:(a2+b2)x2﹣2a2x+a2﹣a2b2=0.
得:(a2+b2)x2﹣2a2x+a2﹣a2b2=0.
△=﹣(2a2)2﹣(a2+b2)(a2﹣a2b2)>0,即a2+b2>1.
x1+x2= ![]() ,y1+y2=﹣( x1+x2)+2=
,y1+y2=﹣( x1+x2)+2= ![]() ,
,
∴點M的坐標為( ![]() ,
, ![]() ).
).
又點M在直線l上,
∴ ![]() ﹣
﹣ ![]() =0,
=0,
∴a2=2b2=2(a2﹣c2),∴a2=2c2,
∴ ![]()
(2)解:由(1)知b=c,設橢圓的右焦點F(b,0)關于直線 ![]() 的對稱點為(x0,y0),
的對稱點為(x0,y0),
由 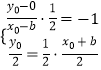 ,解得
,解得 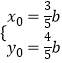
∵x02+y02=1,
∴ ![]() ,
,
∴b2=1,顯然有a2+b2=3>1.
∴所求的橢圓的方程為 ![]()
【解析】(1)設出A、B兩點的坐標,聯立直線與橢圓的方程得關于x的一元二次方程;由根與系數的關系,可得x1+x2 , y1+y2;從而得線段AB的中點坐標,代入直線l的方程,得出a、c的關系,從而求得橢圓的離心率.(2)設橢圓的右焦點坐標為F(b,0),F關于直線l的對稱點為(x0 , y0),則由互為對稱點的連線被對稱軸垂直平分,可得方程組,解得x0、y0;代入圓的方程 x02+y02=1,得出b的值,從而得橢圓的方程.
【考點精析】關于本題考查的橢圓的標準方程,需要了解橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 才能得出正確答案.
才能得出正確答案.


 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:
【題目】設函數y=f(x)的定義域為D,值域為A,如果存在函數x=g(t),使得函數y=f[g(t)]的值域仍是A,那么稱x=g(t)是函數y=f(x)的一個等值域變換.
(1)判斷下列函數x=g(t)是不是函數y=f(x)的一個等值域變換?說明你的理由; ① ![]() ;
;
②f(x)=x2﹣x+1,x∈R,x=g(t)=2t , t∈R.
(2)設f(x)=log2x的定義域為x∈[2,8],已知 ![]() 是y=f(x)的一個等值域變換,且函數y=f[g(t)]的定義域為R,求實數m、n的值.
是y=f(x)的一個等值域變換,且函數y=f[g(t)]的定義域為R,求實數m、n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件樣本,測量這些樣本的一項質量指標值,由測量結果得如下頻數分布表:
質量指標 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
頻數 | 6 | 26 | 38 | 22 | 8 |
則樣本的該項質量指標值落在[105,125]上的頻率為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱 ![]() 中,底面
中,底面 ![]() 是邊長為2的正方形,
是邊長為2的正方形, ![]() 分別為線段
分別為線段 ![]() ,
, ![]() 的中點.
的中點.
(1)求證: ![]() ||平面
||平面 ![]() ;
;
(2)四棱柱 ![]() 的外接球的表面積為
的外接球的表面積為 ![]() ,求異面直線
,求異面直線 ![]() 與
與 ![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一點. 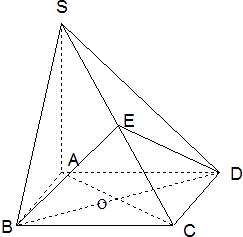
(1)求證:平面EBD⊥平面SAC;
(2)設SA=4,AB=2,求點A到平面SBD的距離;
(3)設SA=4,AB=2,當OE丄SC時,求二面角E﹣BD﹣C余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)是定義在(0,+∞)上的函數,當x>1時,f(x)>0,且滿足 ![]() .
.
(1)求f(1)的值;
(2)判斷并證明函數的單調性;
(3)若f(2)=1,解不等式 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com