
數(shù)列![]() 的各項(xiàng)均為正數(shù),
的各項(xiàng)均為正數(shù),![]() 為其前
為其前![]() 項(xiàng)和,
項(xiàng)和,
對(duì)于任意![]() ,總有
,總有![]() .
.
(1) 求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2) 設(shè)正數(shù)數(shù)列![]() 滿足
滿足![]() ,
,
求數(shù)列![]() 中的最大項(xiàng);
中的最大項(xiàng);
解:(1)由已知:對(duì)于![]() ,總有
,總有![]() ①成立
①成立
∴![]() ②
②
①![]() ②得
②得![]()
∴![]() ∵
∵![]() 均為正數(shù),∴
均為正數(shù),∴![]()
![]()
∴數(shù)列![]() 是公差為1的等差數(shù)列 又
是公差為1的等差數(shù)列 又![]() =1時(shí),
=1時(shí),![]() , 解得
, 解得![]() =1.
=1.
∴![]() . ………………………………………6分
. ………………………………………6分
(2)(解法一)由已知 ![]() ,
,
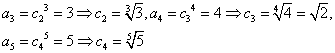
易得 ![]() 猜想
猜想![]() 時(shí),
時(shí),![]() 是遞減數(shù)列............8分
是遞減數(shù)列............8分
令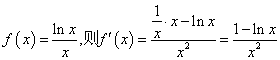
∵當(dāng)![]()
∴在![]() 內(nèi)
內(nèi)![]() 為單調(diào)遞減函數(shù).....................................10分
為單調(diào)遞減函數(shù).....................................10分
由![]() .
.
∴![]() 時(shí),
時(shí), ![]() 是遞減數(shù)列.即
是遞減數(shù)列.即![]() 是遞減數(shù)列.
是遞減數(shù)列.
又![]() , ∴數(shù)列
, ∴數(shù)列![]() 中的最大項(xiàng)為
中的最大項(xiàng)為![]() . ………………………………12分
. ………………………………12分


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
若實(shí)數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() ,則下列命題:
,則下列命題:
(1)若數(shù)列![]() 是遞增數(shù)列,則數(shù)列
是遞增數(shù)列,則數(shù)列![]() 也是遞增數(shù)列;
也是遞增數(shù)列;
(2)數(shù)列![]() 是遞增數(shù)列的充要條件是數(shù)列
是遞增數(shù)列的充要條件是數(shù)列![]() 的各項(xiàng)均為正數(shù);
的各項(xiàng)均為正數(shù);
(3)若![]() 是等比數(shù)列,則
是等比數(shù)列,則![]() 的充要條件是
的充要條件是![]()
其中,正確命題的個(gè)數(shù)是 ( )
A.0個(gè) B.1個(gè) C.2個(gè) D.3個(gè)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年安徽省宿州市高三上學(xué)期期末考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
設(shè)數(shù)列 的各項(xiàng)均為正數(shù),其前n項(xiàng)的和為
的各項(xiàng)均為正數(shù),其前n項(xiàng)的和為 ,對(duì)于任意正整數(shù)m,n,
,對(duì)于任意正整數(shù)m,n,  恒成立.
恒成立.
(Ⅰ)若 =1,求
=1,求 及數(shù)列
及數(shù)列 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)若 ,求證:數(shù)列
,求證:數(shù)列 是等比數(shù)列.
是等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年四川省雙流市外語學(xué)校高三9月月考理科數(shù)學(xué)試卷(解析版) 題型:選擇題
若數(shù)列 的前n項(xiàng)和為
的前n項(xiàng)和為 ,則下列命題:
,則下列命題:
(1)若數(shù)列 是遞增數(shù)列,則數(shù)列
是遞增數(shù)列,則數(shù)列 也是遞增數(shù)列;
也是遞增數(shù)列;
(2)數(shù)列 是遞增數(shù)列的充要條件是數(shù)列
是遞增數(shù)列的充要條件是數(shù)列 的各項(xiàng)均為正數(shù);
的各項(xiàng)均為正數(shù);
(3)若 是等差數(shù)列(公差
是等差數(shù)列(公差 ),則
),則 的充要條件是
的充要條件是
(4)若 是等比數(shù)列,則
是等比數(shù)列,則 的充要條件是
的充要條件是
其中,正確命題的個(gè)數(shù)是( )
A.0個(gè) B.1個(gè) C.2個(gè) D.3個(gè)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省高三下學(xué)期2月聯(lián)考理科數(shù)學(xué) 題型:選擇題
數(shù)列 的各項(xiàng)均為正數(shù),
的各項(xiàng)均為正數(shù), 為其前
為其前 項(xiàng)和,對(duì)于任意
項(xiàng)和,對(duì)于任意 ,總有
,總有 成等差數(shù)列。設(shè)數(shù)列
成等差數(shù)列。設(shè)數(shù)列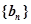 的前
的前 項(xiàng)和為
項(xiàng)和為 ,且
,且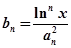 ,則對(duì)任意實(shí)數(shù)
,則對(duì)任意實(shí)數(shù) (
( 是常數(shù),
是常數(shù), )和任意正整數(shù)
)和任意正整數(shù) ,
, 小于的最小正整數(shù)為( ▲ )
小于的最小正整數(shù)為( ▲ )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年福建省高三上學(xué)期11月月考文科數(shù)學(xué)卷 題型:選擇題
數(shù)列 的各項(xiàng)均為正數(shù),
的各項(xiàng)均為正數(shù), 為其前n項(xiàng)和,對(duì)于任意的
為其前n項(xiàng)和,對(duì)于任意的 ,總有
,總有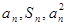 成等差數(shù)列,又記
成等差數(shù)列,又記 ,數(shù)列
,數(shù)列 的前n項(xiàng)和Tn=( )
的前n項(xiàng)和Tn=( )
A.  B.
B.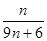 C.
C. D.
D.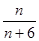
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com