
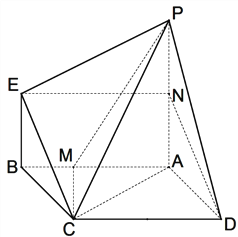
【題目】如圖, ![]() 是平行四邊行,
是平行四邊行, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)證明: ![]() //平面
//平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(4)求二面角![]() 的平面角的正切值.
的平面角的正切值.
【答案】(1)詳見解析;(2)詳見解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】試題分析:(1)取![]() 的中點
的中點![]() ,連
,連![]() ,
, ![]() ,利用平行四邊形得到線線平行,進而利用線面平行的判定定理進行證明;(2)先利用余弦定理、勾股定理證明線線垂直,再利用線面垂直和面面垂直的判定定理進行證明;(3)利用面面垂直的性質作出線面垂直,進而找出線面角;(4)先作出二面角的平面角,再利用直角三角形進行求解.
,利用平行四邊形得到線線平行,進而利用線面平行的判定定理進行證明;(2)先利用余弦定理、勾股定理證明線線垂直,再利用線面垂直和面面垂直的判定定理進行證明;(3)利用面面垂直的性質作出線面垂直,進而找出線面角;(4)先作出二面角的平面角,再利用直角三角形進行求解.
試題解析:(1)取![]() 的中點
的中點![]() ,連
,連![]() ,
, ![]() 。由已知
。由已知![]() //
// ![]() ,
, ![]() ,
, ![]() ,
,
則![]() 為平行四邊形,所以
為平行四邊形,所以![]() //
// ![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]()
(2)![]() 中,
中, ![]() ,
, ![]()
所以![]()
∴![]() ∴
∴![]()
∵![]() 平面
平面![]()
![]() 平面
平面![]()
∴![]() 又∵
又∵![]() ∴
∴![]() 平面
平面![]()
又![]() 平面
平面![]() ∴平面
∴平面![]() 平面
平面![]()
(3)作![]() 于
于![]() ,連
,連![]() ,可證
,可證![]() 平面
平面![]()
![]() 為
為![]() 與平面
與平面![]() 所成角
所成角
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
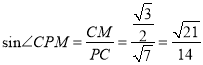 。
。
答: 直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 。
。
(4)![]() .
.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:
【題目】(14分)關于x的不等式ax2+(a﹣2)x﹣2≥0(a∈R)
(1)已知不等式的解集為(﹣∞,﹣1]∪[2,+∞),求a的值;
(2)解關于x的不等式ax2+(a﹣2)x﹣2≥0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一個四位數的各位數字相加和為![]() ,則稱該數為“完美四位數”,如數字“
,則稱該數為“完美四位數”,如數字“![]() ”.試問用數字
”.試問用數字![]() 組成的無重復數字且大于
組成的無重復數字且大于![]() 的“完美四位數”有( )個
的“完美四位數”有( )個
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《數學九章》中對已知三角形三邊長求三角形的面積的求法填補了我國傳統數學的一個空白,與著名的海倫公式完全等價,由此可以看出我國古代已具有很高的數學水平,其求法是:“以小斜冪并大斜冪減中斜冪,余半之,自乘于上.以小斜冪乘大斜冪減上,余四約之,為實.一為從隔,開平方得積.”若把以上這段文字寫成公式,即S= ![]() .現有周長為2
.現有周長為2 ![]() +
+ ![]() 的△ABC滿足sinA:sinB:sinC=(
的△ABC滿足sinA:sinB:sinC=( ![]() ﹣1):
﹣1): ![]() :(
:( ![]() +1),試用以上給出的公式求得△ABC的面積為( )
+1),試用以上給出的公式求得△ABC的面積為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
, ![]() (
(![]() ).
).
(1)求函數![]() 的單調增區間;
的單調增區間;
(2)當![]() 時,記
時,記![]() ,是否存在整數
,是否存在整數![]() ,使得關于
,使得關于![]() 的不等式
的不等式![]() 有解?若存在,請求出
有解?若存在,請求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的方程為![]() +
+![]() =1,A、B為橢圓C的左、右頂點,P為橢圓C上不同于A、B的動點,直線x=4與直線PA、PB分別交于M、N兩點;若D(7,0),則過D、M、N三點的圓必過x軸上不同于點D的定點,其坐標為________.
=1,A、B為橢圓C的左、右頂點,P為橢圓C上不同于A、B的動點,直線x=4與直線PA、PB分別交于M、N兩點;若D(7,0),則過D、M、N三點的圓必過x軸上不同于點D的定點,其坐標為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓柱![]() 底面半徑為1,高為
底面半徑為1,高為![]() ,ABCD是圓柱的一個軸截面,動點M從點B出發沿著圓柱的側面到達點D,其距離最短時在側面留下的曲線
,ABCD是圓柱的一個軸截面,動點M從點B出發沿著圓柱的側面到達點D,其距離最短時在側面留下的曲線![]() 如圖所示.將軸截面ABCD繞著軸
如圖所示.將軸截面ABCD繞著軸![]() 逆時針旋轉
逆時針旋轉![]() 后,邊
后,邊![]() 與曲線
與曲線![]() 相交于點P.
相交于點P.
(Ⅰ)求曲線![]() 長度;
長度;
(Ⅱ)當![]() 時,求點
時,求點![]() 到平面APB的距離;
到平面APB的距離;
(Ⅲ)證明:不存在![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 中,
中, ![]() 是
是![]() 的中點,
的中點, ![]() ,將
,將![]() 沿
沿![]() 折起,使
折起,使![]() 點到達
點到達![]() 點.
點.
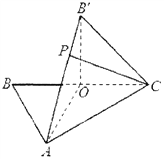
(1)求證: ![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 的體積最大時,試問在線段
的體積最大時,試問在線段![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?若存在,求出點
?若存在,求出點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com