
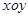 中,曲線
中,曲線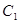 的參數方程為
的參數方程為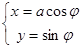 (
(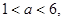
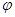 為參數),在以原點
為參數),在以原點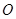 為極點,
為極點,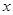 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線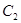 的極坐標方程為
的極坐標方程為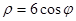 ,射線
,射線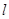 的方程為
的方程為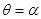 ,又
,又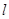 與
與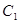 的交點為
的交點為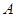 ,
,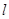 與
與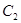 的除極點外的另一個交點為
的除極點外的另一個交點為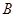 ,當
,當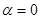 時,
時,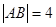 .
.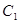 的普通方程,
的普通方程,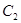 的直角坐標方程;
的直角坐標方程;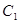 與
與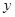 軸正半軸的交點為
軸正半軸的交點為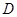 ,當
,當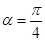 時,求直線
時,求直線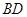 的參數方程.
的參數方程.

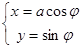 (1<a<6,φ為參數),易消去φ得
(1<a<6,φ為參數),易消去φ得

 時,由x2+ y2-6x=0,y=x得B(3,3)或B(0,0),又B不為極點,∴B(3,3),由(Ⅰ)得D(0,1)
時,由x2+ y2-6x=0,y=x得B(3,3)或B(0,0),又B不為極點,∴B(3,3),由(Ⅰ)得D(0,1) ,∴cosθ=
,∴cosθ= ,sinθ=
,sinθ= ∴直線BD的參數方程為
∴直線BD的參數方程為


科目:高中數學 來源:不詳 題型:解答題
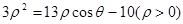
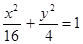 ,設P、Q分別為曲線C1與曲線C2上的任意一點,求|PQ|的最小值.
,設P、Q分別為曲線C1與曲線C2上的任意一點,求|PQ|的最小值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com