
| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 4 |
分析 $\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,利用平面向量的數(shù)量積與夾角公式,結(jié)合正弦定理,即可求出|$\overrightarrow{c}$|的最大值.
解答 解:設(shè)$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.
∵平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$滿足|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,$\overrightarrow{a}$•$\overrightarrow{b}$=-1,
∴cos<$\overrightarrow{a}$$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{-1}{\sqrt{2}×1}$=-$\frac{\sqrt{2}}{2}$,
∴<$\overrightarrow{a}$$\overrightarrow{b}$>=$\frac{3π}{4}$.
∵$\overrightarrow{a}$-$\overrightarrow{c}$與$\overrightarrow{b}$-$\overrightarrow{c}$的夾角為$\frac{π}{4}$,
∴點(diǎn)C在△OAB的外接圓的弦AB所對(duì)的優(yōu)弧上,如圖所示.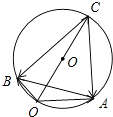
因此|$\overrightarrow{c}$|的最大值為△OAB的外接圓的直徑.
∵|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{{(\sqrt{2})}^{2}-2×(-1){+1}^{2}}$=$\sqrt{5}$.
由正弦定理可得:△OAB的外接圓的直徑2R=$\frac{|\overrightarrow{a}-\overrightarrow{c}|}{sin\frac{3π}{4}}$=$\frac{\sqrt{5}}{\frac{\sqrt{2}}{2}}$=$\sqrt{10}$,
則|$\overrightarrow{c}$|的最大值為$\sqrt{10}$.
故選:A.
點(diǎn)評(píng) 本題考查了向量的夾角公式、三角形法則、數(shù)形結(jié)合的思想方法、正弦定理等基礎(chǔ)知識(shí)與基本技能方法,考查了推理能力,屬于難題.


 同步練習(xí)河南大學(xué)出版社系列答案
同步練習(xí)河南大學(xué)出版社系列答案 同步練習(xí)西南師范大學(xué)出版社系列答案
同步練習(xí)西南師范大學(xué)出版社系列答案 補(bǔ)充習(xí)題江蘇系列答案
補(bǔ)充習(xí)題江蘇系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3x-4y+15=0 | B. | 3x+4y-33=0 | C. | 3x-4y+15=0或x=3 | D. | 3x+4y-33=0或x=3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
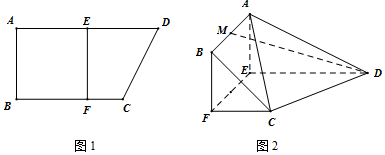
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{17}}{3}$ | D. | $\frac{\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\hat y=x+3$ | B. | $\hat y=x+4$ | C. | $\hat y=2x+3$ | D. | $\hat y=2x+4$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com