已知函數f(x)=|4x-x2|(x∈R),對于任意的正實數t∈(0,b],定義:函數f(x)在[0,t]上的最小值為N(t),函數f(x)在[0,t]上的最大值為M(t),現若存在最小正整數m,使得M(t)-N(t)≤m•t對任意的正實數t∈(0,b]成立,則稱函數f(x)為區間(0,b]的“m階收縮函數”
(1)當t∈(0,1]時,試寫出N(t),M(t)的表達式,并判斷函數f(x)是否為(0,1]上的“m階收縮函數”,如果是,請寫出對應的m的值;(只寫出相應結論,不要求證明過程)
(2)若函數f(x)是(0,b]上的4階收縮函數,求實數b的取值范圍.
解:(1)函數f(x)=|4x-x
2|=|-(x-2)
2+4|,
∵x∈[0,t],t∈(0,1],∴N(t)=0,M(t)=4t-t
2∴M(t)-N(t)=4t-t
2=4t(1-t)≤4•t對t∈(0,1]成立,
則函數f(x)為區間(0,1]的“4階收縮函數”
(2)函數f(x)是(0,b]上的4階收縮函數的意義為:M(t)-N(t)≤4t對任意的正實數t∈(0,b]成立,同時存在t∈(0,b],使得M(t)-N(t)>3t成立
①當0<b<2時,t∈(0,b],N(t)=0,M(t)=4t-t
2∴M(t)-N(t)=4t-t
2=4t(1-t)≤4•t成立,同時存在t∈(0,b],使得M(t)-N(t)>3t成立
②當2≤b<2+2

時,t∈(0,b],N(t)=0,M(t)=
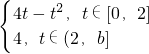
∴t∈[0,2],M(t)-N(t)=4t-t
2≤4•t成立
t∈(2,b],4≤4•t成立,同時存在t∈(0,b],使得M(t)-N(t)=4t-t
2>3t成立
③當b≥2+2

時,t∈(0,b],N(t)=0,M(t)=
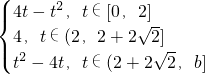
∴t∈[0,2],M(t)-N(t)=4t-t
2≤4•t成立
t∈(2,

],4≤4•t成立,
t
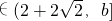
,t
2-4t≤t,∴0≤t≤8
同時存在t∈(0,b],使得M(t)-N(t)=4t-t
2>3t成立
∴0<b≤8時,函數f(x)是(0,b]上的4階收縮函數.
分析:(1)函數f(x)=|4x-x
2|=|-(x-2)
2+4|,根據x∈[0,t],t∈(0,1],可得N(t)=0,M(t)=4t-t
2,從而可知函數f(x)為區間(0,1]的“4階收縮函數”
(2)函數f(x)是(0,b]上的4階收縮函數的意義為:M(t)-N(t)≤4t對任意的正實數t∈(0,b]成立,同時存在t∈(0,b],使得M(t)-N(t)>3t成立.下面進行分類討論:①當0<b<2時,t∈(0,b],N(t)=0,M(t)=4t-t
2成立;②當2≤b<2+2

時,t∈(0,b],N(t)=0,M(t)=
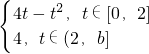
成立;③當b≥2+2

時,t∈(0,b],N(t)=0,M(t)=
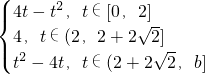
,0≤t≤8成立,故可求b的取值范圍.
點評:本題是典型的信息題,主要考查對新定義的理解,以及敘述的規范性,解題的關鍵是正確運用定義,正確進行分類.

 時,t∈(0,b],N(t)=0,M(t)=
時,t∈(0,b],N(t)=0,M(t)=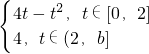
 時,t∈(0,b],N(t)=0,M(t)=
時,t∈(0,b],N(t)=0,M(t)=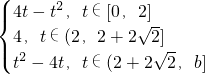
 ],4≤4•t成立,
],4≤4•t成立,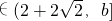 ,t2-4t≤t,∴0≤t≤8
,t2-4t≤t,∴0≤t≤8 時,t∈(0,b],N(t)=0,M(t)=
時,t∈(0,b],N(t)=0,M(t)=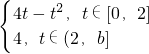 成立;③當b≥2+2
成立;③當b≥2+2 時,t∈(0,b],N(t)=0,M(t)=
時,t∈(0,b],N(t)=0,M(t)=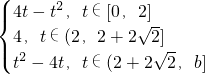 ,0≤t≤8成立,故可求b的取值范圍.
,0≤t≤8成立,故可求b的取值范圍.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案