
已知函數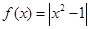 ,
,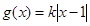 .
.
(Ⅰ)已知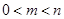 ,若
,若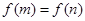 ,求
,求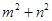 的值;
的值;
(Ⅱ)設 ,當
,當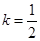 時,求
時,求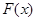 在
在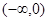 上的最小值;
上的最小值;
(Ⅲ)求函數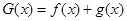 在區間
在區間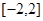 上的最大值.
上的最大值.
(Ⅰ)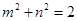 ;(Ⅱ)當
;(Ⅱ)當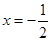 時,
時,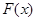 最小值為
最小值為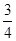 ;(Ⅲ)當
;(Ⅲ)當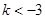 時,
時,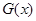 在
在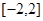 上的最大值為0;當
上的最大值為0;當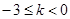 時,
時,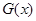 在
在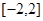 上的最大值為
上的最大值為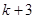 ;當
;當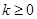 時,
時,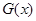 在
在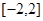 上的最大值為
上的最大值為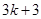 .
.
解析試題分析:(Ⅰ)將函數 去掉絕對值寫成分段函數形式,結合函數圖像滿足
去掉絕對值寫成分段函數形式,結合函數圖像滿足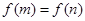 的
的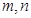 只可能為
只可能為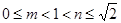 ,從而
,從而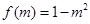 ,
,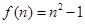 ,由
,由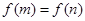 即可得
即可得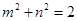 ;(Ⅱ)寫出
;(Ⅱ)寫出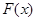 的表達式,根據分段函數的性質,先求出每一段上的最小值,其中最小的即為
的表達式,根據分段函數的性質,先求出每一段上的最小值,其中最小的即為 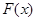 的最小值;(Ⅲ)將
的最小值;(Ⅲ)將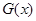 寫成分段函數的形式,每一段均為二次函數的形式,結合二次函數圖像,分類討論函數的對稱軸與區間的關系,從而求出最大值.
寫成分段函數的形式,每一段均為二次函數的形式,結合二次函數圖像,分類討論函數的對稱軸與區間的關系,從而求出最大值.
試題解析:(Ⅰ)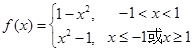
由 圖像可知,
圖像可知,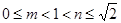
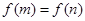 即為
即為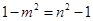 ,所以
,所以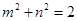 3分
3分
(Ⅱ)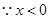 ,則
,則 ,
,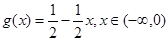
當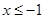 時,
時,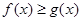 ,即為
,即為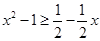 ,解得
,解得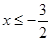
當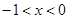 時,
時,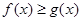 ,即為
,即為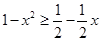 ,解得
,解得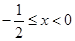
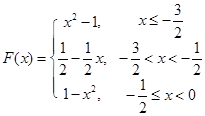
當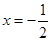 時,
時,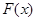 最小值為
最小值為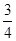
(本問也可直接利用圖像說明理由求解) 6分
(Ⅲ)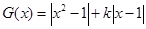
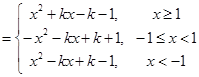
①記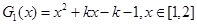 ,結合圖像可知,
,結合圖像可知,
當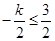 ,即
,即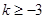 時,
時,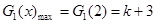
當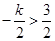 ,即
,即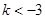 時,
時,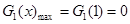 8分
8分
②記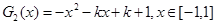 ,結合圖像可知,
,結合圖像可知,
當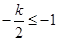 ,即
,即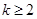 時,
時,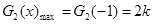
當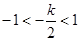 ,即
,即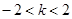 時,
時,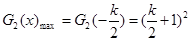 [來源:學*科*網Z*X*X*K]
[來源:學*科*網Z*X*X*K]
當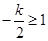 ,即
,即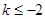 時,
時,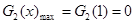
③記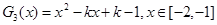 ,結合圖像可知,
,結合圖像可知,
當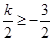 ,即
,即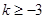 時,
時,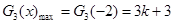
當 ,即
,即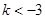 時,
時,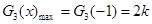 10分
10分
由上討論可知:
當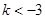 時,
時,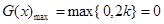
當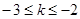 時,
時,
當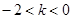 時,
時,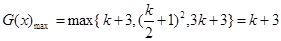
當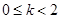 時,
時,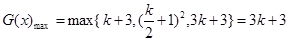
當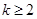 時,
時,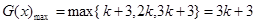 15分
15分
綜上所述:當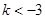 時,
時,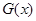 在
在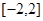 上的最大值為0
上的最大值為0
當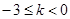 時,
時,

科目:高中數學 來源: 題型:解答題
某種海洋生物身體的長度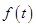 (單位:米)與生長年限t(單位:年)
(單位:米)與生長年限t(單位:年)
滿足如下的函數關系: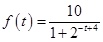 .(設該生物出生時t=0)
.(設該生物出生時t=0)
(1)需經過多少時間,該生物的身長超過8米;
(2)設出生后第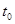 年,該生物長得最快,求
年,該生物長得最快,求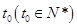 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(14分)已知函數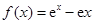 .
.
(Ⅰ)求函數 的最小值;
的最小值;
(Ⅱ)求證: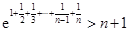
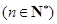 ;
;
(Ⅲ)對于函數 與
與 定義域上的任意實數
定義域上的任意實數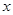 ,若存在常數
,若存在常數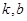 ,使得
,使得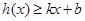 和
和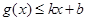 都成立,則稱直線
都成立,則稱直線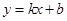 為函數
為函數 與
與 的“分界線”.設函數
的“分界線”.設函數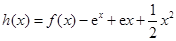 ,
,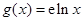 ,
, 與
與 是否存在“分界線”?若存在,求出
是否存在“分界線”?若存在,求出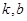 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
運貨卡車以每小時 千米的速度勻速行駛130千米
千米的速度勻速行駛130千米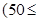
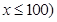 (單位:千米/小時).假設汽油的價格是每升2元,而汽車每小時耗油
(單位:千米/小時).假設汽油的價格是每升2元,而汽車每小時耗油 升,司機的工資是每小時14元.
升,司機的工資是每小時14元.
(1)求這次行車總費用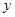 關于
關于 的表達式;
的表達式;
(2)當 為何值時,這次行車的總費用最低,并求出最低費用的值.
為何值時,這次行車的總費用最低,并求出最低費用的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某公園準備建一個摩天輪,摩天輪的外圍是一個周長為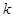 米的圓.在這個圓上安裝座位,且每個座位和圓心處的支點都有一根直的鋼管相連.經預算,摩天輪上的每個座位與支點相連的鋼管的費用為
米的圓.在這個圓上安裝座位,且每個座位和圓心處的支點都有一根直的鋼管相連.經預算,摩天輪上的每個座位與支點相連的鋼管的費用為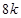 元/根,且當兩相鄰的座位之間的圓弧長為
元/根,且當兩相鄰的座位之間的圓弧長為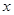 米時,相鄰兩座位之間的鋼管和其中一個座位的總費用為
米時,相鄰兩座位之間的鋼管和其中一個座位的總費用為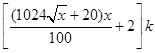 元.假設座位等距離分布,且至少有兩個座位,所有座位都視為點,且不考慮其他因素,記摩天輪的總造價為
元.假設座位等距離分布,且至少有兩個座位,所有座位都視為點,且不考慮其他因素,記摩天輪的總造價為 元.
元.
(Ⅰ)試寫出 關于
關于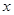 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(Ⅱ)當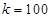 米時,試確定座位的個數,使得總造價最低?
米時,試確定座位的個數,使得總造價最低?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠某種產品的年固定成本為250萬元,每生產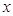 千件,需另投入成本為
千件,需另投入成本為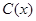 (萬元),當年產量不足80千件時,
(萬元),當年產量不足80千件時,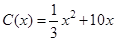 (萬元).當年產量不小于80千件時,
(萬元).當年產量不小于80千件時,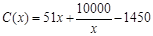 (萬元).每件商品售價為500元.通過市場分析,該廠生產的商品能全部售完.
(萬元).每件商品售價為500元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤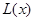 (萬元)關于年產量
(萬元)關于年產量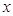 (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com