
某種海洋生物身體的長度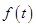 (單位:米)與生長年限t(單位:年)
(單位:米)與生長年限t(單位:年)
滿足如下的函數關系: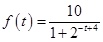 .(設該生物出生時t=0)
.(設該生物出生時t=0)
(1)需經過多少時間,該生物的身長超過8米;
(2)設出生后第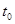 年,該生物長得最快,求
年,該生物長得最快,求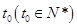 的值.
的值.
(1)6年;(2)4或5.
解析試題分析:(1)求需經過多少時間,該生物的身長超過8米,實質就是解不等式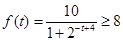 ,不等式解集中的最小值就是本題結論;(2)首先要搞懂什么是“長得最快”,“長得最快”就是說明這一年該生物身體增長的長度最大,因此實質就是求
,不等式解集中的最小值就是本題結論;(2)首先要搞懂什么是“長得最快”,“長得最快”就是說明這一年該生物身體增長的長度最大,因此實質就是求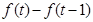 的最大值,即
的最大值,即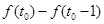 就是這個最大值,下面我們只要求出
就是這個最大值,下面我們只要求出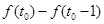 ,分析它的最大值是在
,分析它的最大值是在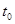 為何值時取得,
為何值時取得,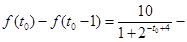
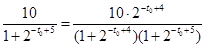 ,此式較繁,因此我們用換元法,設
,此式較繁,因此我們用換元法,設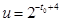 ,由有
,由有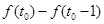
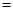
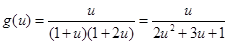 ,它的最大值求法一般是分子分母同時除以
,它的最大值求法一般是分子分母同時除以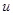 ,然后用基本不等式及不等式的性質得到結論.
,然后用基本不等式及不等式的性質得到結論.
試題解析:(1)設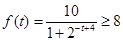 ,即
,即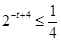 ,解得
,解得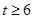 ,
,
即該生物6年后身長可超過8米; 5分
(2)設第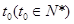 年生長最快,于是有
年生長最快,于是有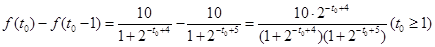 , 8分
, 8分
令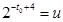 ,則
,則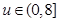 ,
,
令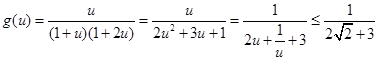 , 11分
, 11分
等號當且僅當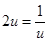 即
即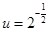 ,
, ,
,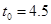 時成立,因為
時成立,因為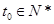 ,因此
,因此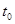 可能值為4或5,由
可能值為4或5,由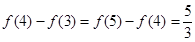 知,所求有年份為第4年和第5年,兩年內各生長了
知,所求有年份為第4年和第5年,兩年內各生長了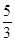 米. 14分
米. 14分
考點:(1)解不等式;(2)換元法與函數的最值.


科目:高中數學 來源: 題型:解答題
設函數f(x)=ax2+bx+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的零點;
(2)若對任意b∈R,函數f(x)恒有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種商品原來每件售價為25元,年銷售8萬件.
(1)據市場調查,若價格每提高1元,銷售量將相應減少2000件,要使銷售的總收入不低于原收入,該商品每件定價最多為多少元?
(2)為了擴大該商品的影響力,提高年銷售量.公司決定明年對該商品進行全面技術革新和營銷策略改革,并提高定價到 元.公司擬投入
元.公司擬投入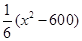 萬元作為技改費用,投入50萬元作為固定宣傳費用,投入
萬元作為技改費用,投入50萬元作為固定宣傳費用,投入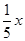 萬元作為浮動宣傳費用.試問:當該商品明年的銷售量
萬元作為浮動宣傳費用.試問:當該商品明年的銷售量 至少應達到多少萬件時,才可能使明年的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
至少應達到多少萬件時,才可能使明年的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com