
設函數(shù)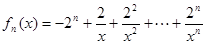 .
.
(1)求函數(shù)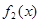 在
在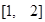 上的值域;
上的值域;
(2)證明對于每一個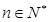 ,在
,在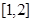 上存在唯一的
上存在唯一的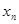 ,使得
,使得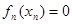 ;
;
(3)求 的值.
的值.
(1) 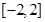 ;(2)證明見解析;(3)當
;(2)證明見解析;(3)當 時,為
時,為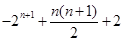 ,當
,當 且
且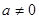 時,為
時,為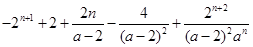 .
.
解析試題分析:(1)由于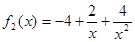 可以看作為
可以看作為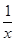 的二次函數(shù),故可利用換元法借助二次函數(shù)知識求出值域;(2)這類問題的常用方法是證明
的二次函數(shù),故可利用換元法借助二次函數(shù)知識求出值域;(2)這類問題的常用方法是證明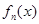 在區(qū)間
在區(qū)間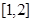 是單調的,且
是單調的,且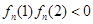 或者
或者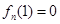 或
或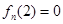 ,即可得證;本題中證
,即可得證;本題中證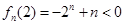 時也可數(shù)學歸納法證明;(3)要求
時也可數(shù)學歸納法證明;(3)要求 的值,注意分類討論,
的值,注意分類討論, 時直接得結論
時直接得結論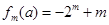 ,那么求
,那么求 時,只要用分組求和即可,在
時,只要用分組求和即可,在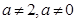 時,
時,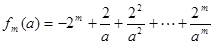 中除第一項外是一個公比不為1的等比數(shù)列的和,因此先求出
中除第一項外是一個公比不為1的等比數(shù)列的和,因此先求出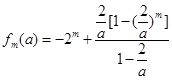
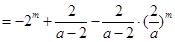 ,同樣在求
,同樣在求 時用分組求和的方法可求得結論.
時用分組求和的方法可求得結論.
試題解析:(1)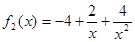 ,由
,由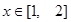 令
令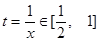 ,
,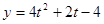 .
.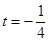 ,
,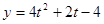 在
在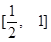 上單調遞增,
上單調遞增,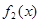 在
在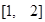 上的值域為
上的值域為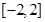 . 4分
. 4分
(2)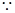 對于
對于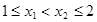 ,
,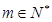 有
有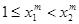 ,
,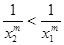 ,從而
,從而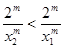 ,
,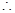
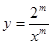 ,
,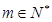 ,在
,在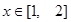 上單調遞減,
上單調遞減,
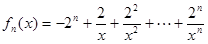 ,
, 在
在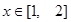 上單調遞減.
上單調遞減.
又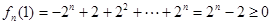 .
.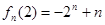 . 7分
. 7分
當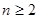 時,
時,
(注用數(shù)學歸納法證明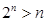 相應給分)
相應給分)
又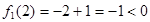 ,即對于任意自然數(shù)
,即對于任意自然數(shù)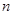 有
有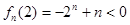
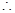 對于每一個
對于每一個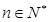 ,存在唯一的
,存在唯一的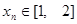 ,使得
,使得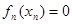 11分
11分
(3)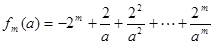 .
.
當 時,
時,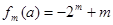 .
.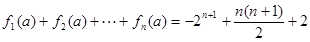 . 14分
. 14分
當 且
且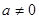 時,
時,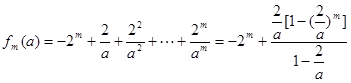 .
.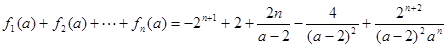 18分
18分
考點:(1)換元法與二次函數(shù)的值域;(2)函數(shù)的零點;(3)分類討論與分組求和.


科目:高中數(shù)學 來源: 題型:解答題
某公司欲建連成片的網球場數(shù)座,用288萬元購買土地20000平方米,每座球場的建筑面積為1000平方米,球場每平方米的平均建筑費用與所建的球場數(shù)有關,當該球場建n座時,每平方米的平均建筑費用 表示,且
表示,且 (其中
(其中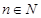 ),又知建5座球場時,每平方米的平均建筑費用為400元.
),又知建5座球場時,每平方米的平均建筑費用為400元.
(1)為了使該球場每平方米的綜合費用最省(綜合費用是建筑費用與購地費用之和),公司應建幾座網球場?
(2)若球場每平方米的綜合費用不超過820元,最多建幾座網球場?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
近日,國家經貿委發(fā)出了關于深入開展增產節(jié)約運動,大力增產市場適銷對路產品的通知,并發(fā)布了當前國內市場185種適銷工業(yè)品和42種滯銷產品的參考目錄。為此,一公司舉行某產品的促銷活動,經測算該產品的銷售量P萬件(生產量與銷售量相等)與促銷費用x萬元滿足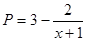 (其中
(其中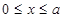 ,a為正常數(shù));已知生產該產品還需投入成本(10+2P)萬元(不含促銷費用),產品的銷售價格定為
,a為正常數(shù));已知生產該產品還需投入成本(10+2P)萬元(不含促銷費用),產品的銷售價格定為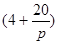 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤y萬元表示為促銷費用x萬元的函數(shù);
(2)促銷費用投入多少萬元時,廠家的利潤是大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設 ,
, .
.
(Ⅰ)證明: ;
;
(Ⅱ)求證:在數(shù)軸上,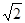 介于
介于 與
與 之間,且距
之間,且距 較遠;
較遠;
(Ⅲ)在數(shù)軸上,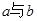 之間的距離是否可能為整數(shù)?若有,則求出這個整數(shù);若沒有,
之間的距離是否可能為整數(shù)?若有,則求出這個整數(shù);若沒有,
說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)
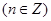 滿足
滿足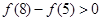 .
.
(1)求 的解析式;
的解析式;
(2)對于(1)中得到的函數(shù) ,試判斷是否存在
,試判斷是否存在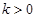 ,使
,使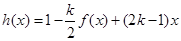 在區(qū)間
在區(qū)間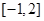 上的值域為
上的值域為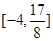 ?若存在,求出
?若存在,求出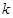 ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某種海洋生物身體的長度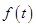 (單位:米)與生長年限t(單位:年)
(單位:米)與生長年限t(單位:年)
滿足如下的函數(shù)關系: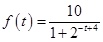 .(設該生物出生時t=0)
.(設該生物出生時t=0)
(1)需經過多少時間,該生物的身長超過8米;
(2)設出生后第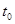 年,該生物長得最快,求
年,該生物長得最快,求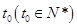 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
有一塊邊長為4米的正方形鋼板,現(xiàn)對其進行切割,焊接成一個長方體無蓋容器(切、焊損耗忽略不計),有人用數(shù)學知識作了如下設計:在鋼板的四個角處各切去一個小正方形,剩余部分圍成長方體。
(Ⅰ)求這種切割、焊接而成的長方體的最大容積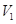 .
.
(Ⅱ)請問:能重新設計,使所得長方體的容器的容積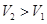 嗎?若能、給出你的一種設計方案。
嗎?若能、給出你的一種設計方案。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
運貨卡車以每小時 千米的速度勻速行駛130千米
千米的速度勻速行駛130千米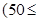
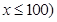 (單位:千米/小時).假設汽油的價格是每升2元,而汽車每小時耗油
(單位:千米/小時).假設汽油的價格是每升2元,而汽車每小時耗油 升,司機的工資是每小時14元.
升,司機的工資是每小時14元.
(1)求這次行車總費用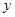 關于
關于 的表達式;
的表達式;
(2)當 為何值時,這次行車的總費用最低,并求出最低費用的值.
為何值時,這次行車的總費用最低,并求出最低費用的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)=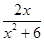 .
.
(1)若f(x)>k的解集為{x|x<-3,或x>-2},求k的值;
(2)對任意x>0,f(x)≤t恒成立,求t的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com