
【題目】已知雙曲線x2﹣ ![]() =1的左右焦點分別為F1、F2 , 過點F2的直線交雙曲線右支于A,B兩點,若△ABF1是以A為直角頂點的等腰三角形,則△AF1F2的面積為 .
=1的左右焦點分別為F1、F2 , 過點F2的直線交雙曲線右支于A,B兩點,若△ABF1是以A為直角頂點的等腰三角形,則△AF1F2的面積為 .
 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:高中數學 來源: 題型:
【題目】將函數 ![]() 的圖像向左平移
的圖像向左平移 ![]() 個單位,再向上平移1個單位,得到g(x)的圖像.若g(x1)g(x2)=9,且x1 , x2∈[﹣2π,2π],則2x1﹣x2的最大值為( )
個單位,再向上平移1個單位,得到g(x)的圖像.若g(x1)g(x2)=9,且x1 , x2∈[﹣2π,2π],則2x1﹣x2的最大值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是( )
A.y=sinx的圖象向右平移![]() 個單位得y=cosx的圖象
個單位得y=cosx的圖象
B.y=cosx的圖象向右平移![]() 個單位得y=sinx的圖象
個單位得y=sinx的圖象
C.當φ>0時,y=sinx的圖象向右平移φ個單位可得y=sin(x+φ)的圖象
D.當φ<0時,y=sinx的圖象向左平移φ個單位可得y=sin(x﹣φ)的圖象
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x1 , x2是方程e﹣x+2=|lnx|的兩個解,則( )
A.0<x1x2< ![]()
B.![]() <x1x2<1
<x1x2<1
C.1<x1x2<e
D.x1x2>e
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
設f(x)=|ax﹣1|.
(Ⅰ)若f(x)≤2的解集為[﹣6,2],求實數a的值;
(Ⅱ)當a=2時,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤7﹣3m成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lnx﹣ax2+ax,a為正實數.
(1)當a=2時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)求證:f( ![]() )≤0;
)≤0;
(3)若函數f(x)有且只有1個零點,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑. 如圖,在陽馬P﹣ABCD中,側棱PD⊥底面ABCD,且PD=CD,E為PC中點,點F在PB上,且PB⊥平面DEF,連接BD,BE.
(Ⅰ)證明:DE⊥平面PBC;
(Ⅱ)試判斷四面體DBEF是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
(Ⅲ)已知AD=2, ![]() ,求二面角F﹣AD﹣B的余弦值.
,求二面角F﹣AD﹣B的余弦值.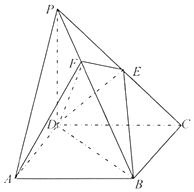
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓 ![]() 的左右頂點分別為A,B,點P在橢圓上且異于A,B兩點,O為坐標原點.
的左右頂點分別為A,B,點P在橢圓上且異于A,B兩點,O為坐標原點.
(1)若直線AP與BP的斜率之積為 ![]() ,求橢圓的離心率;
,求橢圓的離心率;
(2)若|AP|=|OA|,證明直線OP的斜率k滿足|k|> ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com