
【題目】過橢圓E:![]() 1(a>b>0)上一動點P向圓O:x2+y2=b2引兩條切線PA,PB,切點分別是A,B.直線AB分別與x軸,y軸交于點M,N(O為坐標原點).
1(a>b>0)上一動點P向圓O:x2+y2=b2引兩條切線PA,PB,切點分別是A,B.直線AB分別與x軸,y軸交于點M,N(O為坐標原點).

(1)若在橢圓E上存在點P,滿足PA⊥PB,求橢圓E的離心率的取值范圍;
(2)求證:在橢圓E內,存在一點C滿足|CO|=|CA|=|CP|=|CB|;
(3)若橢圓E的短軸長為2,△MON面積的最小值為![]() ,求橢圓E的方程.
,求橢圓E的方程.
【答案】(1)[![]() ,1);(2)見解析(3)
,1);(2)見解析(3)![]() .
.
【解析】
(1)由題意可知![]() ,又由
,又由![]() ,得
,得![]() ,因為
,因為![]() ,列出不等式求解即可得到本題答案;
,列出不等式求解即可得到本題答案;
(2)當點C為OP得中點時,由直角三角形的性質:斜邊上的中線等于斜邊的一半,即可得到點C符合題意;
(3)由題意可知![]() ,設出點P坐標,求出以
,設出點P坐標,求出以![]() 為直徑的圓的方程,與圓O的方程相減得過切點
為直徑的圓的方程,與圓O的方程相減得過切點![]() 的直線方程,再求出點
的直線方程,再求出點![]() 的坐標,進而求出
的坐標,進而求出![]() ,再求出點O到直線MN的距離d,所以
,再求出點O到直線MN的距離d,所以![]() ,再結合點P在橢圓
,再結合點P在橢圓![]() 上以及基本不等式,得到
上以及基本不等式,得到![]() ,從而求得
,從而求得![]() ,即可得到本題答案.
,即可得到本題答案.
(1)∵![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴橢圓E的離心率的取值范圍為: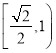 ;
;
(2)證明:當點C為OP的中點時,
∵直線PA與直線PB都和圓O相切,
∴![]() 都是直角三角形,
都是直角三角形,
∴![]() ,∴
,∴![]() ,
,
故在橢圓E內,存在一點C滿足![]() ;
;
(3)由題意可知![]() ,設點
,設點![]() ,
,
∴以![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() ,與圓O的方程
,與圓O的方程![]() 相減得:
相減得:![]() ,
,
∴過切點![]() 的直線方程為:
的直線方程為:![]() ,
,
令![]() 得,
得,![]() ,∴
,∴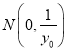 ;令
;令![]() 得,
得,![]() ,∴
,∴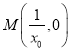 ,
,
∴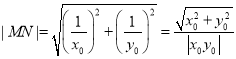 ,
,
∵點O到直線MN的距離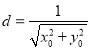 ,
,
∴![]() ,
,
∵點P在橢圓![]() 上,
上,
∴![]() ,當且僅當
,當且僅當![]() 時取等號,
時取等號,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴橢圓E的方程為:![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖是2018年第一季度五省GDP情況圖,則下列陳述中不正確的是
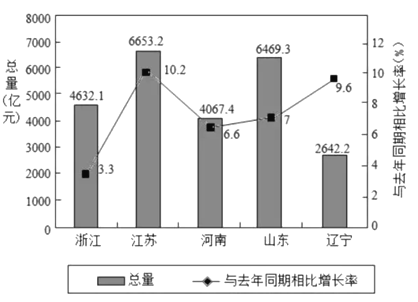
A. 2018年第一季度GDP增速由高到低排位第5的是浙江省
B. 與2017年同期相比,各省2018年第一季度的GDP總量實現了增長
C. 2017年同期河南省的GDP總量不超過4000億元
D. 2018年第一季度GDP總量和增速由高到低排位均居同一位的省只有1個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海關對同時從A,B,C三個不同地區進口的某種商品進行抽樣檢測,從各地區進口此種商品的數量(單位:件)如表所示.工作人員用分層抽樣的方法從這些商品中共抽取6件樣品進行檢測.
地區 | A | B | C |
數量 | 50 | 150 | 100 |
(1)求這6件樣品中來自A,B,C各地區商品的數量;
(2)若在這6件樣品中隨機抽取2件送往甲機構進行進一步檢測,求這2件商品來自相同地區的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,函數
,函數![]() 是定義在
是定義在![]() 上的奇函數,且滿足
上的奇函數,且滿足![]() .
.
(Ⅰ)確定![]() 與
與![]() 的關系式,并求
的關系式,并求![]() 的解析式.
的解析式.
(Ⅱ)若數列![]() 的前
的前![]() 項和為
項和為![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,是否存在實數
,是否存在實數![]() ,使得對于任意的
,使得對于任意的![]() ,都有
,都有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019超長“三伏”來襲,雖然大部分人都了解“伏天”不宜吃生冷食物,但隨著氣溫的不斷攀升,仍然無法阻擋冷飲品銷量的暴增.現在,某知名冷飲品銷售公司通過隨機抽樣的方式,得到其100家加盟超市3天內進貨總價的統計結果如下表所示:
組別(單位:百元) |
|
|
|
|
|
|
頻數 | 3 | 11 | 20 | 27 | 26 | 13 |
(1)由頻數分布表大致可以認為,被抽查超市3天內進貨總價![]() ,μ近似為這100家超市3天內進貨總價的平均值(同一組中的數據用該組區間的中點值作代表),利用正態分布,求
,μ近似為這100家超市3天內進貨總價的平均值(同一組中的數據用該組區間的中點值作代表),利用正態分布,求![]() ;
;
(2)在(1)的條件下,該公司為增加銷售額,特別為這100家超市制定如下抽獎方案:
①令m表示“超市3天內進貨總價超過μ的百分點”,其中![]() .若
.若![]() ,則該超市獲得1次抽獎機會;
,則該超市獲得1次抽獎機會;![]() ,則該超市獲得2次抽獎機會;
,則該超市獲得2次抽獎機會;![]() ,則該超市獲得3次抽獎機會;
,則該超市獲得3次抽獎機會;![]() ,則該超市獲得4次抽獎機會;
,則該超市獲得4次抽獎機會;![]() ,則該超市獲得5次抽獎機會;
,則該超市獲得5次抽獎機會;![]() ,則該超市獲得6次抽獎機會.另外,規定3天內進貨總價低于μ的超市沒有抽獎機會;
,則該超市獲得6次抽獎機會.另外,規定3天內進貨總價低于μ的超市沒有抽獎機會;
②每次抽獎中獎獲得的獎金金額為1000元,每次抽獎中獎的概率為![]() .
.
設超市A參加了抽查,且超市A在3天內進貨總價![]() 百元.記X(單位:元)表示超市A獲得的獎金總額,求X的分布列與數學期望.
百元.記X(單位:元)表示超市A獲得的獎金總額,求X的分布列與數學期望.
附參考數據與公式:![]() ,若
,若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com