
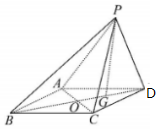
 四棱錐P-ABCD中,四邊形ABCD為平行四邊形,AC與BD交于點O,點G為BD上一點,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
四棱錐P-ABCD中,四邊形ABCD為平行四邊形,AC與BD交于點O,點G為BD上一點,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$. 分析 利用向量的三角形法則、平行四邊形法則即可得出.
解答 解:$\overrightarrow{PG}$=$\overrightarrow{PB}+\overrightarrow{BG}$=$\overrightarrow{PB}+\frac{2}{3}\overrightarrow{BD}$=$\overrightarrow{PB}+\frac{2}{3}$$(\overrightarrow{BA}+\overrightarrow{BC})$=$\overrightarrow{PB}$+$\frac{2}{3}(\overrightarrow{PA}-\overrightarrow{PB}+\overrightarrow{PC}-\overrightarrow{PB})$=$\frac{2}{3}$$\overrightarrow{PA}-\frac{1}{3}\overrightarrow{PB}$+$\frac{2}{3}\overrightarrow{PC}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
故答案為:$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
點評 本題考查了向量的三角形法則、平行四邊形法則及其運算性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | “am2<bm2”是“a<b”的充分不必要條件 | |
| B. | 命題“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$” | |
| C. | 若p,q均為假命題,則p∧q為假命題 | |
| D. | 若ζ~B(4,0.25),則Dξ=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}+1$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
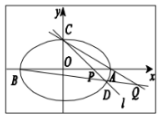 過點C(0,$\sqrt{2}$)的橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,橢圓與x軸交于兩點A(a,0),B(-a,0),過點C的直線l與橢圓交于另一點D,并與x軸交于點P,直線AC與BD交于點Q.
過點C(0,$\sqrt{2}$)的橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,橢圓與x軸交于兩點A(a,0),B(-a,0),過點C的直線l與橢圓交于另一點D,并與x軸交于點P,直線AC與BD交于點Q.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
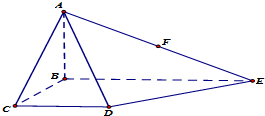 如圖,在四棱錐A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,點F為AE的中點.
如圖,在四棱錐A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,點F為AE的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | c>b>a | B. | b>c>a | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com