【題目】已知函數
.
(1)討論函數
的單調性；
(2)判斷函數能否有3個零點？若能，求出
的取值范圍；若不能，請說明理由.
【答案】（1）見解析；（2）不可能有
個零點；說明見解析
【解析】
（1）求導后，根據導函數零點的分布情況在
不同的取值范圍情況下討論導函數的正負，從而得到函數的單調性；（2）采用反證法，假設有個零點，可知需滿足
或
；當時，可得極大值
，從而知不可能有個零點；當時，可得極大值
，將其看做關于的函數，通過導數可判斷出
，從而可知不可能有個零點；可知假設錯誤，即
不可能有個零點.
（1）由題意知：函數定義域為
①若
，則
當
時，
，則為減函數
當
時，
，則為增函數
②若
當
或時，，則為增函數
當
時，，則為減函數
③若
，則
，故在上增函數
④若
當或
時，，則為增函數
當
時，，則為減函數
（2）若函數有個零點，由（1）可知，必有或
①若，由（1）可知在
處取得極大值，在
處取得極小值
此時不可能有個零點
②若，由（1）可知在處取得極大值，在處取得極小值
則
，
，即
在
上單調遞增
在上單調遞減
當
時，
此時不可能有個零點
綜上所述：函數不可能有個零點
科目：高中數學 來源： 題型：
【題目】有甲、乙兩家公司都需要招聘求職者,這兩家公司的聘用信息如下：
甲公司 | 乙公司 | ||||||||
職位 | A | B | C | D | 職位 | A | B | C | D |
月薪/千元 | 5 | 6 | 7 | 8 | 月薪/千元 | 4 | 6 | 8 | 10 |
獲得相應職位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 獲得相應職位概率 | 0.4 | 0.3 | 0.2 | 0.1 |
（1）若兩人分別去應聘甲、乙兩家公司的C職位，記這兩人被甲、乙兩家公司的C職位錄用的人數和為
，求的分布列；
（2）根據甲、乙兩家公司的聘用信息，如果你是該求職者,你會選擇哪一家公司？說明理由。
（3）若小王和小李分別被甲、乙兩家公司錄用，求小王月薪高于小李的概率。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一只藥用昆蟲的產卵數
與一定范圍內與溫度
有關, 現收集了該種藥用昆蟲的6組觀測數據如下表：
溫度 | 21 | 23 | 24 | 27 | 29 | 32 |
產卵數 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用線性回歸模型，求關于的回歸方程
=
x+
（精確到0.1）；
(2)若用非線性回歸模型求關的回歸方程為 
且相關指數
( i )試與 (1)中的線性回歸模型相比，用
說明哪種模型的擬合效果更好.
( ii )用擬合效果好的模型預測溫度為
時該種藥用昆蟲的產卵數（結果取整數）.
附：一組數據(x1,y1), (x2,y2), ...,(xn,yn), 其回歸直線=x+的斜率和截距的最小二乘估計為
，
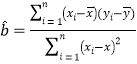，相關指數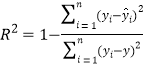
．
。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】己知橢圓
的焦距為
，以橢圓C的右頂點A為圓心的圓與直線
相交于P，Q兩點，且
．
(I)求橢圓C的標準方程和圓A的方程。
(II)不過原點的直線l與橢圓C交于M，N兩點，已知直線OM，l，ON的斜率
成等比數列，記以線段OM，線段ON為直徑的圓的面積分別為
的值是否為定值?若是，求出此值：若不是，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“剪刀、石頭、布”的游戲規則是：雙方齊喊口令，然后同時出拳，握緊的拳頭代表“石頭”，“食指和中指伸出代表“剪刀”，五指伸開代表“布”。“ 石頭”勝“剪刀”， “剪刀”勝“布”， “布”勝“石頭”，若所出拳相同則為和局。現甲乙兩人通過“剪刀、石頭、布”進行比賽。
（1）設甲乙兩人每局都隨機出“剪刀”、“石頭”、“布”中的某一個，求甲勝乙的概率；
（2）最近中國科學家在網上發布了“剪刀、石頭、布”的致勝策略，引起了甲的關注，據甲認真觀察，乙有以下出拳習慣：①第一局不出“剪刀”； ②連續兩局的出拳一定不一樣，即如本局出“剪刀”，則下局出“石頭”、“布”中的一個。假設甲的分析是正確的，甲據此分析出拳，保證每局都不輸給乙，在最多5局的比賽中，誰勝的局數多，誰獲勝。游戲結束的條件是：一方勝3局或賽滿5局，用
表示游戲結束時的游戲局數，求的分布列和期望。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠家擬舉行促銷活動，經調查測算，該產品的年銷售量（即該廠的年產量）
萬件與年促銷費用
萬元（
）滿足
（
為常數），如果不搞促銷活動，則該產品的年銷售量只能是1萬件.已知年生產該產品的固定投入為8萬元，每生產1萬件該產品需要再投入16萬元，廠家將每件產品的銷售價格定為每件產品年平均成本的1.5倍（產品成本包括固定投入和再投入兩部分資金）.
（1）將該產品的年利潤
萬元表示為年促銷費用萬元的函數；
（2）該廠家年促銷費用投入多少萬元時，廠家的利潤最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
為偶函數，函數
為奇函數。
對任意實數x恒成立.
（1）求函數與；
（2）設
，
，若
對于
恒成立，求實數m的取值范圍；
（3）對于（2）中的函數
，若方程
沒有實數解，實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
