
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).
為參數).
(Ⅰ)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設曲線![]() 經過伸縮變換
經過伸縮變換 得到曲線
得到曲線![]() ,若點
,若點![]() ,直線
,直線![]() 與
與![]() 交與
交與![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x-4y+3=0.
(1)若圓C的切線在x軸和y軸上的截距相等,求此切線的方程.
(2)從圓C外一點P(x1,y1)向該圓引一條切線,切點為M,O為坐標原點,且有|PM|=|PO|,求使得|PM|取得最小值的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱柱ABOA′B′O′中,∠AOB=90°,側棱OO′⊥面OAB,OA=OB=OO′=2.若C為線段O′A的中點,在線段BB′上求一點E,使|EC|最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某顏料公司生產![]() 、
、![]() 兩種產品,其中生產每噸
兩種產品,其中生產每噸![]() 產品,需要甲染料
產品,需要甲染料![]() 噸,乙染料
噸,乙染料![]() 噸,丙染料
噸,丙染料![]() 噸,生產每噸
噸,生產每噸![]() 產品,需要甲染料
產品,需要甲染料![]() 噸,乙染料
噸,乙染料![]() 噸,丙染料
噸,丙染料![]() 噸,且該公司一天之內甲、乙、丙三種染料的用量分別不超過
噸,且該公司一天之內甲、乙、丙三種染料的用量分別不超過![]() 噸、
噸、![]() 噸、
噸、![]() 噸,如果
噸,如果![]() 產品的利潤為
產品的利潤為![]() 元/噸,
元/噸, ![]() 產品的利潤為
產品的利潤為![]() 元/噸,則該顏料公司一天內可獲得的最大利潤為( )
元/噸,則該顏料公司一天內可獲得的最大利潤為( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,E、F為棱AD、AB的中點. 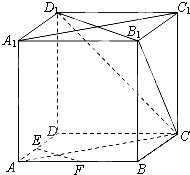
(1)求證:EF∥平面CB1D1;
(2)求證:平面CAA1C1⊥平面CB1D1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
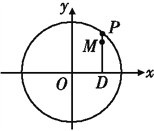
【題目】如圖,設P是圓![]() 上的動點,點D是P在x軸上的投影,M為線段PD上一點,且
上的動點,點D是P在x軸上的投影,M為線段PD上一點,且![]() ,
,
(1)當P在圓上運動時,求點M的軌跡C的方程;
(2)求過點(3,0)且斜率為![]() 的直線被軌跡C所截線段的長度.
的直線被軌跡C所截線段的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com