
【題目】已知函數![]() (
(![]() ).
).
(1)當![]() 時,討論
時,討論![]() 的單調性;
的單調性;
(2)求![]() 在區間
在區間![]() 上的最小值.
上的最小值.
【答案】(1)![]() 的增區間為
的增區間為![]() ,
,![]() ,減區間為
,減區間為![]() ;(2)當
;(2)當![]() 時,
時,![]() 的最小值為
的最小值為![]() ;當
;當![]() 時,
時,![]() 的最小值為
的最小值為![]() ;當
;當![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
【解析】
試題分析:(1)研究單調性,可求出導函數![]() ,然后解不等式
,然后解不等式![]() 得單調增區間,解不等式
得單調增區間,解不等式![]() 得減區間,注意絕對值,要分類求解;(2)由于
得減區間,注意絕對值,要分類求解;(2)由于![]() ,因此先分類
,因此先分類![]() ,
,![]() ,
,![]() ,前兩種情形,絕對值符號直接去掉,因此只要用導數
,前兩種情形,絕對值符號直接去掉,因此只要用導數![]() 研究單調性可得最值,第三種情形同樣要去絕對值符號,只是此時是分段函數,
研究單調性可得最值,第三種情形同樣要去絕對值符號,只是此時是分段函數,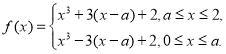 ,
,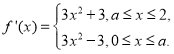 ,可以看出這時又要分類:
,可以看出這時又要分類:![]() ,
,![]() ,得單調性再得最小值.
,得單調性再得最小值.
試題解析:(1)當![]() 時,
時,![]() .
.
①當![]() 時,
時,![]() ,
,![]() ,
,
∴![]() 在
在![]() 單調遞增;
單調遞增;
②當![]() 時,
時,![]() ,
,![]() .
.
![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 單調遞減;
單調遞減;
![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 單調遞增.
單調遞增.
綜上,![]() 的增區間為
的增區間為![]() ,
,![]() ,減區間為
,減區間為![]() .
.
(2)①![]() 時,
時,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
②![]() 時,
時,![]() ,
,![]() ,
,
![]() ,
,![]() 在
在![]() 單調遞增,
單調遞增,
∴![]() .
.
③![]() 時,而
時,而![]() ,
,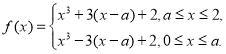
∴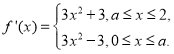
(i)![]() 時,
時,![]() 在
在![]() 上單增,
上單增,![]() 為最小值.
為最小值.
![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上單調遞減,
上單調遞減,
∴![]() .
.
(ii)![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() .
.
在![]() 時,
時,![]() ,
,
∴![]() .
.
綜上可知,當![]() 時,
時,![]() 的最小值為
的最小值為![]() ;當
;當![]() 時,
時,![]() 的最小值為
的最小值為![]() ;當
;當![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() ,計算數列
,計算數列![]() 的第100項.
的第100項.
現已給出該問題算法的流程圖(如圖1所示)

(1)請在圖1中判斷框的![]() (其中
(其中![]() 中用
中用![]() 的關系表示)處填上合適的語句,使之完成該問題的算法功能.
的關系表示)處填上合適的語句,使之完成該問題的算法功能.
(2)根據流程圖1補充完整程序語言(如圖2)(即在![]() 處填寫合適的語句).
處填寫合適的語句).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga![]() (a>0,且a≠1)
(a>0,且a≠1)
(1)判斷f(x)的奇偶性并證明;
(2)若對于x∈[2,4],恒有f(x)>loga![]() 成立,求m的取值范圍.
成立,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記![]() ,若
,若![]() ,
,![]() 均是定義在實數集R上的函數,定義函數
均是定義在實數集R上的函數,定義函數![]() =
=![]() ,則下列命題正確的是( )
,則下列命題正確的是( )
A.若![]() ,
,![]() 都是單調函數,則
都是單調函數,則![]() 也是單調函數
也是單調函數
B.若![]() ,
,![]() 都是奇函數,則
都是奇函數,則![]() 也是奇函數
也是奇函數
C.若![]() ,
,![]() 都是偶函數,則
都是偶函數,則![]() 也是偶函數
也是偶函數
D.若![]() 是奇函數,
是奇函數,![]() 是偶函數,則
是偶函數,則![]() 既不是奇函數,也不是偶函數
既不是奇函數,也不是偶函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】側棱垂直于底面的棱柱叫做直棱柱.
側棱不垂直于底面的棱柱叫作斜棱柱.
底面是正多邊形的直棱柱叫作正棱柱.
底面是平行四邊形的四棱柱叫作平行六面體.
側棱與底面垂直的平行六面體叫作直平行六面體.
底面是矩形的直平行六面體叫作長方體.
棱長都相等的長方體叫作正方體.
請根據上述定義,回答下面的問題(填“一定”、“不一定”“一定不”):
(1)直四棱柱________是長方體;
(2)正四棱柱________是正方體.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() ,底面
,底面![]() 是
是![]() 的菱形,側面
的菱形,側面![]() 是邊長為
是邊長為![]() 的正三角形,O是AD的中點,
的正三角形,O是AD的中點, ![]() 為
為![]() 的中點.
的中點.

(1)求證:![]() ;
;
(2)若PO與底面ABCD垂直,求直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點P(-1,2,3)關于xOz平面對稱的點的坐標是 ( )
A. (1,2,3) B. (-1,-2,3)
C. (-1,2,-3) D. (1,-2,-3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)判斷函數![]() 的奇偶性,并加以證明;
的奇偶性,并加以證明;
(2)用定義證明函數![]() 在區間
在區間![]() 上為增函數;
上為增函數;
(3)若函數![]() 在區間
在區間![]() 上的最大值與最小值之和不小于
上的最大值與最小值之和不小于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】社區服務是綜合實踐活動課程的重要內容,某市教育部門在全市高中學生中隨機抽取200位學生參加社區服務的數據,按時間段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:小時)進行統計,其頻率分布直方圖如圖所示.
(單位:小時)進行統計,其頻率分布直方圖如圖所示.
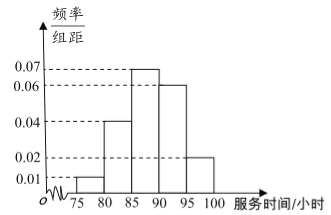
(1)求抽取的200位學生中,參加社區服務時間不少于90小時的學生人數,并估計從全市高中學生中任意選取一人,其參加社區服務時間不少于90小時的概率;
(2)從全市高中學生(人數很多)中任意選取3位學生,記![]() 為3位學生中參加社區服務時間不少于90小時的人數,試求隨機變量
為3位學生中參加社區服務時間不少于90小時的人數,試求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com