【題目】已知函數
，
.
（1）若
，求
的最值；
（2）若當
時，
，求m的取值范圍.
【答案】（1）
的最小值為
，無最大值；（2）
.
【解析】
（1）對函數進行求導，判斷函數的單調性，結合函數的單調性進行求解即可；
（2）對已知的不等式進行化簡，然后構造新函數，對新函數求導，分類討論，結合零點的定義進行求解即可.
（1）的定義域為R，
，
因為當
時，
，當
時，
，
所以在
上遞減，在
上遞增，
所以若
，則的最小值為
，無最大值.
（2）由已知，得當
時，
，
即
，即
恒成立，
令
，則
，
，
，
設
，
，
由（1）知
在
上遞增，
①若
，則當
時，
，則
在上遞增，
所以當時，
，所以
在上遞增，
所以當時，
，符合題意.
②若
，則
，
，
，
因為在上遞增，
所以在上有唯一零點（記為
），且當
時，
，
所以在
上遞減，
所以當時，
，所以在上遞減，
所以當時，
，不合題意.
綜上，m的取值范圍為.
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，橢圓
左、右焦點分別為
，
，離心率為
，兩準線間距離為8，圓O的直徑為
，直線l與圓O相切于第四象限點T，與y軸交于M點，與橢圓C交于點N（N點在T點上方），且
．
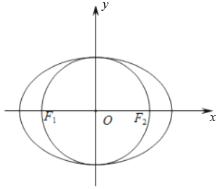
（1）求橢圓C的標準方程；
（2）求直線l的方程；
（3）求直線l上滿足到，距離之和為
的所有點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝（x﹣1）2﹣alnx（a＜0）.
（1）討論f（x）的單調性；
（2）若f（x）存在兩個極值點x1，x2（x1＜x2），且關于x的方程f（x）＝b（b∈R）恰有三個實數根x3，x4，x5（x3＜x4＜x5），求證：2（x2﹣x1）＞x5﹣x3.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國是茶的故鄉，也是茶文化的發源地.中國茶的發現和利用已有四千七百多年的歷史，且長盛不衰，傳遍全球.為了弘揚中國茶文化，某酒店推出特色茶食品“金萱排骨茶”，為了解每壺“金萱排骨茶”中所放茶葉量
克與食客的滿意率
的關系，通過試驗調查研究，發現可選擇函數模型
來擬合與的關系，根據以下數據：
茶葉量 | 1 | 2 | 3 | 4 | 5 |
| 4.34 | 4.36 | 4.44 | 4.45 | 4.51 |
可求得y關于x的回歸方程為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C：
（
）的焦點為F，過F且斜率為1的直線與C交于A，B兩點，
.
（1）求C的方程；
（2）過點
的直線l交C于點M，N，點Q為
的中點，
軸交C于點R，且
，證明：動點T在定直線上.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】端午節是我國民間為紀念愛國詩人屈原的一個傳統節日.某市為了解端午節期間粽子的銷售情況，隨機問卷調查了該市1000名消費者在去年端午節期間的粽子購買量（單位：克），所得數據如下表所示：
購買量 |
|
|
|
|
|
人數 | 100 | 300 | 400 | 150 | 50 |
將煩率視為概率
（1）試求消費者粽子購買量不低于300克的概率；
（2）若該市有100萬名消費者，請估計該市今年在端午節期間應準備多少千克棕子才能滿足市場需求（以各區間中點值作為該區間的購買量）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對任意實數
給出下列命題:①“
”是“
”的充要條件;②“
是無理數”是“
是無理數”的充要條件;③“
”是“
”的充分條件;④“
”是“
”的必要條件.其中真命題的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司對旗下的甲、乙兩個門店在1至9月份的營業額（單位：萬元）進行統計并得到如圖折線圖.
下面關于兩個門店營業額的分析中，錯誤的是( )
A.甲門店的營業額折線圖具有較好的對稱性，故而營業額的平均值約為32萬元
B.根據甲門店的營業額折線圖可知，該門店營業額的平均值在[20，25]內
C.根據乙門店的營業額折線圖可知，其營業額總體是上升趨勢
D.乙門店在這9個月份中的營業額的極差為25萬元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
