
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是邊長為1的菱形,
是邊長為1的菱形,![]() ,
,![]() 面
面![]() ,
,![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
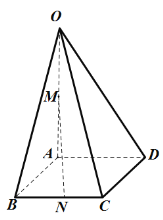
(1)證明:直線![]() 平面
平面![]() ;
;
(2)求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)證明見解析(2)![]() (3)
(3)![]()
【解析】
(1) 取![]() 的中點
的中點![]() ,構造平行四邊形
,構造平行四邊形![]() ,再根據線面平行的判定定理完成證明;
,再根據線面平行的判定定理完成證明;
(2)根據平行可知異面直線![]() 與
與![]() 所成的角即為
所成的角即為![]() 或其補角,然后根據長度進行求解;
或其補角,然后根據長度進行求解;
(3)根據線面平行將問題轉化為![]() 到平面
到平面![]() 的距離,然后作出
的距離,然后作出![]() 在平面內的射影,根據長度即可計算出
在平面內的射影,根據長度即可計算出![]() 到平面
到平面![]() 的距離,即可求解出點
的距離,即可求解出點![]() 到平面
到平面![]() 的距離.
的距離.
(1)取![]() 的中點
的中點![]() ,連接
,連接![]() 、
、![]() .則四邊形
.則四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() ,又∵
,又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
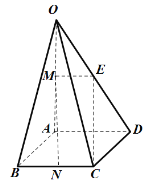
(2)∵![]() ,
,
∴![]() 為異面直線
為異面直線![]() 與
與![]() 所成的角(或其補角)
所成的角(或其補角)
作![]() 于點
于點![]() ,連接
,連接![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
所以異面直線![]() 與
與![]() 所成的角為
所成的角為![]() .
.

(3)∵![]() 平面
平面![]() ,∴點
,∴點![]() 和點
和點![]() 到平面
到平面![]() 的距離相等.
的距離相等.
連接![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
線段![]() 的長就是點
的長就是點![]() 到平面
到平面![]() 的距離,與點
的距離,與點![]() 到平面
到平面![]() 的距離相等
的距離相等
![]() ,
,![]() ,
,
 .
.
所以點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.



科目:高中數學 來源: 題型:
【題目】如圖①,在等腰梯形![]() 中,
中,![]() 分別為
分別為![]() 的中點
的中點![]()
![]() 為
為![]() 中點,現將四邊形
中點,現將四邊形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如圖②所示的多面體,在圖②中.
,得到如圖②所示的多面體,在圖②中. 
(1)證明:![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(-1,0),B(1,0),C(0,1),直線y=ax+b(a>0)將△ABC分割為面積相等的兩部分,則b的取值范圍是________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,錯誤的是( )
A.一條直線和直線外一點確定一個平面
B.平行于同一平面的兩個不同平面平行
C.若直線![]() 不平行平面
不平行平面![]() ,則在平面
,則在平面![]() 內不存在與
內不存在與![]() 平行的直線
平行的直線
D.如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 內一定不存在直線垂直于平面
內一定不存在直線垂直于平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在邊長為3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .將梯形
.將梯形![]() 沿直線
沿直線![]() 折起,使
折起,使![]() 平面
平面![]() ,如圖2,
,如圖2,![]() 分別是
分別是![]() 上的點.
上的點.

(1)求證:圖2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有五張卡片,其中紅色卡片三張,標號分別為1,2,3;藍色卡片兩張,標號分別為1,2.
(1)將紅色卡片和藍色卡片分別放在兩個袋中,然后從兩個袋中各取一張卡片,求兩張卡片數字之積為偶數的概率
(2)將五張卡片放在一個袋子中,從中任取兩張,求兩張卡片顏色不同的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com