
分析 (1)曲線C1在平面直角坐標系中的參數方程為$\left\{\begin{array}{l}{x=\frac{\sqrt{5}}{5}t}\\{y=\frac{2\sqrt{5}}{5}t-1}\end{array}\right.$(t為參數),消去參數t可得普通方程.由曲線C2:ρ=2cosθ-4sinθ,即ρ2=ρ(2cosθ-4sinθ),利用互化公式可得直角坐標方程.
(2)x2+y2=2x-4y.化為(x-1)2+(y+2)2=5.可得圓心C2(1,-2),半徑r=$\sqrt{5}$.求出圓心到直線的距離d,可得曲線C1和C2兩交點之間的距離=2$\sqrt{{r}^{2}-p9vv5xb5^{2}}$.
解答 解:(1)曲線C1在平面直角坐標系中的參數方程為$\left\{\begin{array}{l}{x=\frac{\sqrt{5}}{5}t}\\{y=\frac{2\sqrt{5}}{5}t-1}\end{array}\right.$(t為參數),消去參數t可得普通方程:y=2x-1.
由曲線C2:ρ=2cosθ-4sinθ,即ρ2=ρ(2cosθ-4sinθ),可得直角坐標方程:x2+y2=2x-4y.
(2)x2+y2=2x-4y.化為(x-1)2+(y+2)2=5.可得圓心C2(1,-2),半徑r=$\sqrt{5}$.
∴曲線C1和C2兩交點之間的距離=2$\sqrt{5-(\frac{2+2-1}{\sqrt{{1}^{2}+{2}^{2}}})^{2}}$=$\frac{8\sqrt{5}}{5}$.
點評 本題考查了參數方程化為普通方程、極坐標方程化為直角坐標方程、直線與圓相交弦長問題、點到直線的距離公式,考查了推理能力與計算能力,屬于中檔題.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
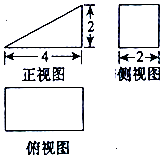
| A. | $20+4\sqrt{5}$ | B. | $12+4\sqrt{5}$ | C. | $20+2\sqrt{5}$ | D. | $12+2\sqrt{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com