
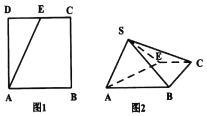
【題目】如圖,點E為正方形ABCD邊CD上異于點C、D的動點,將△ADE沿AE翻折成△SAE,在翻折過程中,下列三個說法中正確的個數(shù)是( )
①存在點E和某一翻折位置使得AE∥平面SBC;
②存在點E和某一翻折位置使得SA⊥平面SBC;
③二面角S﹣AB﹣E的平面角總是小于2∠SAE.
A.0B.1C.2D.3
【答案】B
【解析】
對于①,四邊形ABCE為梯形,所以AE與BC必然相交;對于②,假設SA![]() 平面SBC,可推得矛盾;對于③,當將△ADE沿AE翻折使得平面SAE⊥平面ABCE時,二面角S﹣AB﹣E最大,在平面SAE內(nèi),作出一個角等于二面角S﹣AB﹣E的平面角;由角
平面SBC,可推得矛盾;對于③,當將△ADE沿AE翻折使得平面SAE⊥平面ABCE時,二面角S﹣AB﹣E最大,在平面SAE內(nèi),作出一個角等于二面角S﹣AB﹣E的平面角;由角![]() 所在三角形的一個外角,它是不相鄰的兩個內(nèi)角之和,結(jié)合圖形,即可判定③.
所在三角形的一個外角,它是不相鄰的兩個內(nèi)角之和,結(jié)合圖形,即可判定③.
對于①,四邊形ABCE為梯形,所以AE與BC必然相交,故①錯誤;
對于②,假設SA![]() 平面SBC,SC
平面SBC,SC![]() 平面SBC,所以SA⊥SC,又SA⊥SE,SE∩SC=S,所以SA⊥平面SCE,所以平面SCE∥平面SBC,這與平面SBC∩平面SCE=SC矛盾,
平面SBC,所以SA⊥SC,又SA⊥SE,SE∩SC=S,所以SA⊥平面SCE,所以平面SCE∥平面SBC,這與平面SBC∩平面SCE=SC矛盾,
故假設不成立,即②錯誤;
對于③,當將△ADE沿AE翻折使得平面SAE⊥平面ABCE時,二面角S﹣AB﹣E最大,如圖,在平面SAE內(nèi),作SO⊥AE,垂足為O,∴SO⊥平面ABCE;AB![]() 平面ABCE,
平面ABCE,
所以SO⊥AB;
作OF⊥AB,垂足為F,連接SF,SO∩OF=O,則AB⊥平面SFO,所以AB⊥SF,則∠SFG即為二面角S﹣AB﹣E的平面角;
在直線AE上取一點![]() ,使得O
,使得O![]() =OF,連接S
=OF,連接S![]() ,則∠S
,則∠S![]() O=∠SFO;
O=∠SFO;
由圖形知,在△SA![]() 中,S
中,S![]() >A
>A![]() ,所以∠AS
,所以∠AS![]() <∠SAE;而∠S
<∠SAE;而∠S![]() O=∠SAE+∠AS
O=∠SAE+∠AS![]() ,
,
故∠S![]() O<2∠SAE;
O<2∠SAE;
即∠SFO<2∠SAE.故③正確.
故選:B.


 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】若數(shù)列![]() 同時滿足條件:①存在互異的
同時滿足條件:①存在互異的![]() 使得
使得![]() (
(![]() 為常數(shù));
為常數(shù));
②當![]() 且
且![]() 時,對任意
時,對任意![]() 都有
都有![]() ,則稱數(shù)列
,則稱數(shù)列![]() 為雙底數(shù)列.
為雙底數(shù)列.
(1)判斷以下數(shù)列![]() 是否為雙底數(shù)列(只需寫出結(jié)論不必證明);
是否為雙底數(shù)列(只需寫出結(jié)論不必證明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)設![]() ,若數(shù)列
,若數(shù)列![]() 是雙底數(shù)列,求實數(shù)
是雙底數(shù)列,求實數(shù)![]() 的值以及數(shù)列
的值以及數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)設![]() ,是否存在整數(shù)
,是否存在整數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 為雙底數(shù)列?若存在,求出所有的
為雙底數(shù)列?若存在,求出所有的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某中學2018年的高考考生人數(shù)是2015年高考考生人數(shù)的![]() 倍,為了更好地對比該校考生的升學情況,統(tǒng)計了該校2015年和2018年的高考情況,得到如圖柱狀圖:
倍,為了更好地對比該校考生的升學情況,統(tǒng)計了該校2015年和2018年的高考情況,得到如圖柱狀圖:

則下列結(jié)論正確的是![]()
![]()
A. 與2015年相比,2018年一本達線人數(shù)減少
B. 與2015年相比,2018年二本達線人數(shù)增加了![]() 倍
倍
C. 2015年與2018年藝體達線人數(shù)相同
D. 與2015年相比,2018年不上線的人數(shù)有所增加
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
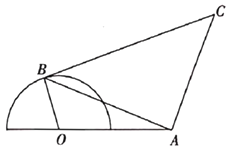
【題目】某生態(tài)農(nóng)莊有一塊如圖所示的空地,其中半圓O的直徑為300米,A為直徑延長線上的點,![]() 米,B為半圓上任意一點,以AB為一邊作等腰直角
米,B為半圓上任意一點,以AB為一邊作等腰直角![]() ,其中BC為斜邊.
,其中BC為斜邊.
![]() 若
若![]() ;,求四邊形OACB的面積;
;,求四邊形OACB的面積;
![]() 現(xiàn)決定對四邊形OACB區(qū)域地塊進行開發(fā),將
現(xiàn)決定對四邊形OACB區(qū)域地塊進行開發(fā),將![]() 區(qū)域開發(fā)成垂釣中心,預計每平方米獲利10元,將
區(qū)域開發(fā)成垂釣中心,預計每平方米獲利10元,將![]() 區(qū)域開發(fā)成親子采摘中心,預計每平方米獲利20元,則當
區(qū)域開發(fā)成親子采摘中心,預計每平方米獲利20元,則當![]() 為多大時,垂釣中心和親子采摘中心獲利之和最大?
為多大時,垂釣中心和親子采摘中心獲利之和最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,且
為矩形,且![]() 平面
平面![]() ,
,![]() .
.
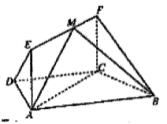
(1)求證:![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上運動,當點
上運動,當點![]() 在什么位置時,平面
在什么位置時,平面![]() 與平面
與平面![]() 所成銳二面角最大,并求此時二面角的余弦值.
所成銳二面角最大,并求此時二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知四棱錐S﹣ABCD的底面為矩形,SA⊥底面ABCD,點E在線段BC上,以AD為直徑的圓過點 E.若SA=![]() AB=3,則△SED面積的最小值為_____.
AB=3,則△SED面積的最小值為_____.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com