
【題目】若數列![]() 同時滿足條件:①存在互異的
同時滿足條件:①存在互異的![]() 使得
使得![]() (
(![]() 為常數);
為常數);
②當![]() 且
且![]() 時,對任意
時,對任意![]() 都有
都有![]() ,則稱數列
,則稱數列![]() 為雙底數列.
為雙底數列.
(1)判斷以下數列![]() 是否為雙底數列(只需寫出結論不必證明);
是否為雙底數列(只需寫出結論不必證明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)設![]() ,若數列
,若數列![]() 是雙底數列,求實數
是雙底數列,求實數![]() 的值以及數列
的值以及數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)設![]() ,是否存在整數
,是否存在整數![]() ,使得數列
,使得數列![]() 為雙底數列?若存在,求出所有的
為雙底數列?若存在,求出所有的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1) ①③是雙底數列,②不是雙底數列(2) ![]()
![]() (3)存在整數
(3)存在整數![]() 或
或![]() ,使得數列
,使得數列![]() 為雙底數列
為雙底數列
【解析】試題分析:(1)根據雙底數列的定義可判定①③是雙底數列,②不是雙底數列;(2)由雙底數列定義可知![]() ,解得
,解得![]() , 當
, 當![]() 時,數列成等差,
時,數列成等差, ![]() ,當
,當![]() 時,
時, ![]() ,從而可得結果;(3)
,從而可得結果;(3)![]() , 若數列
, 若數列![]() 是雙底數列,則
是雙底數列,則![]() 有解(否則不是雙底數列),即
有解(否則不是雙底數列),即 ![]() ,該方程共有四組解,分別驗證是否為雙底數列即可得結果.
,該方程共有四組解,分別驗證是否為雙底數列即可得結果.
試題解析:(1)①③是雙底數列,②不是雙底數列;
(2)數列![]() 當
當![]() 時遞減,當
時遞減,當![]() 時遞增,
時遞增,
由雙底數列定義可知![]() ,解得
,解得![]() ,
,
當![]() 時,數列成等差,
時,數列成等差, ![]() ,
,
當![]() 時,
時, ![]()
![]() ,
,
綜上, ![]() .
.
(3)![]() ,
,
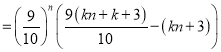
![]() ,
,
若數列![]() 是雙底數列,則
是雙底數列,則![]() 有解(否則不是雙底數列),
有解(否則不是雙底數列),
即 ![]() ,
,
得![]() 或
或![]() 或
或![]() 或
或![]()
故當![]() 時,
時, ![]() ,
,
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;
;
從而 ![]() ,數列
,數列![]() 不是雙底數列;
不是雙底數列;
同理可得:
當![]() 時,
時, ![]() ,數列
,數列![]() 不是雙底數列;
不是雙底數列;
當![]() 時,
時, ![]() ,數列
,數列![]() 是雙底數列;
是雙底數列;
當![]() 時,
時, ![]() ,數列
,數列![]() 是雙底數列;
是雙底數列;
綜上,存在整數![]() 或
或![]() ,使得數列
,使得數列![]() 為雙底數列.
為雙底數列.


科目:高中數學 來源: 題型:
【題目】中國詩詞大會的播出引發(fā)了全民讀書熱,某學校語文老師在班里開展了一次詩詞默寫比賽,班里40名學生得分數據的莖葉圖如右圖,若規(guī)定得分不低于85分的學生得到“詩詞達人”的稱號,低于85分且不低于70分的學生得到“詩詞能手”的稱號,其他學生得到“詩詞愛好者”的稱號.根據該次比賽的成績按照稱號的不同進行分層抽樣抽選10名學生,則抽選的學生中獲得“詩詞能手”稱號的人數為( )

A. 6B. 5C. 4D. 2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩地相距![]() 海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為
海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為![]() ,其他費用為每小時
,其他費用為每小時![]() 元,且該貨輪的最大航行速度為
元,且該貨輪的最大航行速度為![]() 海里/小時.
海里/小時.
(![]() )請將該貨輪從甲地到乙地的運輸成本
)請將該貨輪從甲地到乙地的運輸成本![]() 表示為航行速度
表示為航行速度![]() (海里/小時)的函數.
(海里/小時)的函數.
(![]() )要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
)要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=sin 2x+![]() cos 2x圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將圖象上所有點向右平移
cos 2x圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將圖象上所有點向右平移![]() 個單位長度,得到函數g(x)的圖象,則g(x)圖象的一條對稱軸方程是( )
個單位長度,得到函數g(x)的圖象,則g(x)圖象的一條對稱軸方程是( )
A. x=-![]() B. x=
B. x=![]()
C. x=![]() D. x=
D. x=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M為AA1的中點,P是BC上的一點,且由P沿棱柱側面經過棱CC1到M的最短路線長為![]() ,設這條最短路線與CC1的交點為N.求:
,設這條最短路線與CC1的交點為N.求:

(1)該三棱柱的側面展開圖的對角線的長;
(2)PC和NC的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,曲線![]() :
: ![]() 經過伸縮變換
經過伸縮變換![]() 后得到曲線
后得到曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求出曲線![]() 、
、![]() 的參數方程;
的參數方程;
(Ⅱ)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 、
、![]() 上的動點,求
上的動點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
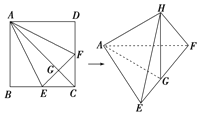
【題目】如圖,在正方形ABCD中,E、F分別是BC、CD的中點,G是EF的中點,現在沿AE、AF及EF把這個正方形折成一個空間圖形,使B、C、D三點重合,重合后的點記為H,那么,在這個空間圖形中必有( )
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中數學 來源: 題型:
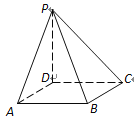
【題目】在四棱錐P–ABCD中,底面ABCD是邊長為6的正方形,PD平面ABCD,PD=8.
(1) 求PB與平面ABCD所成角的大小;
(2) 求異面直線PB與DC所成角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com