
【題目】已知橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,它的一個頂點恰好是拋物線
,它的一個頂點恰好是拋物線![]() 的焦點.
的焦點.

(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 與橢圓交于
與橢圓交于![]() 兩點,
兩點,![]() 點位于第一象限,
點位于第一象限,![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側的動點.
兩側的動點.
(i)若直線![]() 的斜率為
的斜率為![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
(ii)當點![]() 運動時,滿足
運動時,滿足![]() ,問直線
,問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
【答案】(I)![]() ;(Ⅱ)(i)
;(Ⅱ)(i)![]() ;(ii)
;(ii)![]() 的斜率為定值
的斜率為定值![]() .
.
【解析】
試題(I)設橢圓![]() 的方程為
的方程為![]() ,由條件利用橢圓的性質求得
,由條件利用橢圓的性質求得![]() 和
和![]() 的值,可得橢圓
的值,可得橢圓![]() 的方程.
的方程.
(II)(i)設![]() 的方程為
的方程為![]() ,代入橢圓
,代入橢圓![]() 的方程化簡,由△>0,求得
的方程化簡,由△>0,求得![]() 的范圍,再利用利用韋達定理可得
的范圍,再利用利用韋達定理可得![]() 以及
以及![]() 的值.再求得
的值.再求得![]() 的坐標,根據四邊形
的坐標,根據四邊形![]() 的面積
的面積![]() ,計算求得結果.
,計算求得結果.
(ii)當![]() 時,C、
時,C、![]() 的斜率之和等于零,
的斜率之和等于零,![]() 的方程為
的方程為![]() ,把它代入橢圓
,把它代入橢圓![]() 的方程化簡求得
的方程化簡求得![]() .再把直線
.再把直線![]() 的方程橢圓
的方程橢圓![]() 的方程化簡求得
的方程化簡求得![]() 的值,可得
的值,可得![]() 以及
以及![]() 的值,從而求得
的值,從而求得![]() 的斜率
的斜率![]() 的值.
的值.
試題解析:設橢圓![]() 的方程為
的方程為![]() ,由題意可得它的一個頂點恰好是拋物線
,由題意可得它的一個頂點恰好是拋物線![]() 的焦點
的焦點![]() ,
,![]() .
.
再根據離心率![]() ,求得
,求得![]() ,∴橢圓C的方程為
,∴橢圓C的方程為![]() .
.
(Ⅱ)(i)設![]() ,
,![]() 的方程為
的方程為![]() ,代入橢圓
,代入橢圓![]() 的方程化簡可得
的方程化簡可得![]() ,由
,由![]() ,求得
,求得![]() .
.
利用韋達定理可得![]() ,
,![]() .
.
在![]() 中,令
中,令![]() 求得
求得![]() ,∴四邊形
,∴四邊形![]() 的面積
的面積
![]()
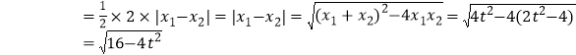 ,
,
故當![]() 時,四邊形
時,四邊形![]() 的面積
的面積![]() 取得最小值為4.
取得最小值為4.
(ii)當![]() 時,
時,![]() 、
、![]() 的斜率之和等于零,設
的斜率之和等于零,設![]() 的斜率為
的斜率為![]() ,則
,則![]() 的斜率為
的斜率為![]() ,
,
![]() 的方程為
的方程為![]() ,把它代入橢圓
,把它代入橢圓![]() 的方程化簡可得
的方程化簡可得
![]() ,所以
,所以![]() .
.
同理可得直線![]() 的方程為
的方程為![]() ,
,
![]() ,
,
![]() 的斜率
的斜率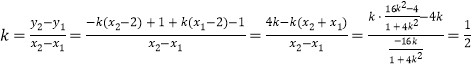 .
.


 新編小學單元自測題系列答案
新編小學單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】《九章算術》中“竹九節”問題:現有一根9節的竹子,自上而下各節的容積成等差數列,上面4節的容積共3升,下面3節的容積共4升,則第6節的容積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(﹣2,0),B(0,1)在橢圓C: ![]() (a>b>0)上.
(a>b>0)上.
(Ⅰ)求橢圓C的方程;
(Ⅱ)P是線段AB上的點,直線y= ![]() x+m(m≥0)交橢圓C于M、N兩點,若△MNP是斜邊長為
x+m(m≥0)交橢圓C于M、N兩點,若△MNP是斜邊長為 ![]() 的直角三角形,求直線MN的方程.
的直角三角形,求直線MN的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,a、b、c分別是角A、B、C的對邊,若A滿足2cos2A+cos(2A+ ![]() )=﹣
)=﹣ ![]() .
.
(Ⅰ)求A的值;
(Ⅱ)若c=3,△ABC的面積為3 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的函數y=f(x)為減函數,且函數y=f(x﹣1)的圖象關于點(1,0)對稱,若f(x2﹣2x)+f(2b﹣b2)≤0,且0≤x≤2,則x﹣b的取值范圍是( )
A.[﹣2,0]
B.[﹣2,2]
C.[0,2]
D.[0,4]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校某文具商店經營某種文具,商店每銷售一件該文具可獲利3元,若供大于求則削價處理,每處理一件文具虧損1元;若供不應求,則可以從外部調劑供應,此時每件文具僅獲利2元.為了了解市場需求的情況,經銷商統計了去年一年(52周)的銷售情況.
銷售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
周數 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
以去年每周的銷售量的頻率為今年每周市場需求量的概率.
(1)要使進貨量不超過市場需求量的概率大于0.5,問進貨量的最大值是多少?
(2)如果今年的周進貨量為14,寫出周利潤Y的分布列;
(3)如果以周利潤的期望值為考慮問題的依據,今年的周進貨量定為多少合適?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,離心率為
,離心率為![]() ,并過點
,并過點![]() .
.
(1)求橢圓方程;
(2)若直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點(
兩點(![]() 不是左右頂點),且以
不是左右頂點),且以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 的右頂點。求證:直線
的右頂點。求證:直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義![]() 為n個正數
為n個正數![]() 的“均倒數”.已知正項數列{an}的前n項的“均倒數”為
的“均倒數”.已知正項數列{an}的前n項的“均倒數”為![]() .
.
(1)求數列{an}的通項公式.
(2)設數列![]() 的前n項和為
的前n項和為![]() ,若4
,若4![]() <
<![]() 對一切
對一切![]() 恒成立試求實數m的取值范圍.
恒成立試求實數m的取值范圍.
(3)令![]() ,問:是否存在正整數k使得
,問:是否存在正整數k使得![]() 對一切
對一切![]() 恒成立,如存在求出k值,否則說明理由.
恒成立,如存在求出k值,否則說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com