直線l過橢圓
＝1(a＞b＞0)的右焦點F，方向向量為v＝(a，b)，若原點到直線l的距離是右焦點到右準線距離，則橢圓的離心率為________．
桃李文化快樂暑假武漢出版社系列答案
優秀生快樂假期每一天全新寒假作業本系列答案
暑假接力賽新疆青少年出版社系列答案科目：高中數學 來源：2011屆高考數學第一輪復習測試題1 題型：044
如圖，斜率為k的直線l過橢圓
＝1(a＞b＞0)對稱軸上的定點D(λa，0)(λ為非零常數，λ≠±1)，且l交橢圓于A、B兩點．
(1)當k＝λ＝
，且線段AB中點的橫坐標等于
時，求橢圓的離心率；
(2)試探究：在x軸上是否存在定點M，使
·
恒為定值？
查看答案和解析>>
科目：高中數學 來源：浙江省臺州中學2012屆高三下學期第二次統練數學理科試題 題型：044
已知方向向量為
＝
的直線l過橢圓
的焦點以及點(0，
)，直線l與橢圓C交于A、B兩點，且A、B兩點與另一焦點圍成的三角形周長為
．
(1)求橢圓C的方程；
(2)過左焦點F1且不與x軸垂直的直線m交橢圓于M、N兩點，
·
＝
≠0(O坐標原點)，求直線m的方程．
查看答案和解析>>
科目：高中數學 來源：2011-2012學年安徽省安慶市高三第二次模擬考試文科數學試卷（解析版） 題型：解答題
已知：橢圓C：
＝1（a＞b＞0）的左、右焦點為F1、F2，e＝
，過F1的直線l交橢圓C于A、B兩點，｜AF2｜、｜AB｜、｜BF2｜成等差數列，且｜AB｜＝4。
（I）求橢圓C的方程；
（II）M、N是橢畫C上的兩點，若線段MN被直線x＝1平分，證明：線段MN的中垂線過定點。
查看答案和解析>>
科目：高中數學 來源：2013屆四川省高二上學期期中理科數學試卷 題型：解答題
已知橢圓的長軸長為2a，焦點是F1(－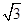
，0)、F2(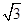，0)，點F1到直線x＝－
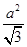的距離為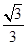
，過點F2且傾斜角為銳角的直線l與橢圓交于A、B兩點，使得|F2B|＝3|F2A|.
(1)求橢圓的方程；
(2)求直線l的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
