
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且滿足(2c﹣a)cosB﹣bcosA=0.
(Ⅰ)求角B的大小;
(Ⅱ)求 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )的取值范圍.
)的取值范圍.
【答案】解:(Ⅰ)在△ABC中,∵(2c﹣a)cosB﹣bcosA=0,∴2sinCcosB﹣sinAcosB﹣sinBcosA=0, 即2sinCcosB﹣sin(A+B)=0,
即sinC(2cosB﹣1)=0,
∴cosB= ![]() ,
,
∴B= ![]() .
.
(Ⅱ)由(Ⅰ)可得 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )=
)= ![]() sinA+cosA=2sin(A+
sinA+cosA=2sin(A+ ![]() ),
),
∵A∈(0, ![]() ),
),
∴A+ ![]() ∈(
∈( ![]() ,
, ![]() ),sin(A+
),sin(A+ ![]() )∈(
)∈( ![]() ,1],
,1],
∴2sin(A+ ![]() )∈(1,2],即
)∈(1,2],即 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )的取值范圍是(1,2]
)的取值范圍是(1,2]
【解析】(Ⅰ)在△ABC中,由條件利用正弦定理、兩角和差的正弦公式可得 sinC(2cosB﹣1)=0,故有cosB= ![]() ,由此求得 B的值.(Ⅱ)由(Ⅰ)可得
,由此求得 B的值.(Ⅱ)由(Ⅰ)可得 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )=2sin(A+
)=2sin(A+ ![]() ),根據A∈(0,
),根據A∈(0, ![]() ),利用正弦函數的定義域和值域求得
),利用正弦函數的定義域和值域求得 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )的取值范圍.
)的取值范圍.


科目:高中數學 來源: 題型:
【題目】如圖,已知AB⊥平面BCD,BC⊥CD,AD與平面BCD所成的角為30°,且AB=BC=2; 
(1)求三棱錐A﹣BCD的體積;
(2)設M為BD的中點,求異面直線AD與CM所成角的大小(結果用反三角函數值表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓Γ: ![]() +
+ ![]() =1(a>b>0)的離心率與雙曲線x2﹣y2=a2的離心率之和為
=1(a>b>0)的離心率與雙曲線x2﹣y2=a2的離心率之和為 ![]() ,B1、B2為橢圓Γ短軸的兩個端點,P是橢圓Γ上一動點(不與B1、B2重合),直線B1P、B2P分別交直線l:y=4于M、N兩點,△B1B2P的面積記為S1 , △PMN的面積記為S2 , 且S1的最大值為4
,B1、B2為橢圓Γ短軸的兩個端點,P是橢圓Γ上一動點(不與B1、B2重合),直線B1P、B2P分別交直線l:y=4于M、N兩點,△B1B2P的面積記為S1 , △PMN的面積記為S2 , 且S1的最大值為4 ![]() .
.
(1)求橢圓Γ的方程;
(2)若S2=λS1 , 當λ取最小值時,求點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC中,角A,B,C的對邊分別為a,b,c,且三角形的面積S= ![]() accosB.
accosB.
(1)求角B的大小;
(2)若a=2 ![]() ,點D在AB的延長線上,且AD=3,cos∠ADC=
,點D在AB的延長線上,且AD=3,cos∠ADC= ![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某年高考中,某省10萬考生在滿分為150分的數學考試中,成績分布近似服從正態分布N(110,100),則分數位于區間(130,150]分的考生人數近似為( ) (已知若X~N(μ,σ2),則P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544,P(μ﹣3σ<X<μ+3σ)=0.9974.
A.1140
B.1075
C.2280
D.2150
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】牛頓法求方程f(x)=0近似根原理如下:求函數y=f(x)在點(xn , f(xn))處的切線y=f′(xn)(x﹣xn)+f(xn),其與x軸交點橫坐標xn+1=xn﹣ ![]() (n∈N*),則xn+1比xn更靠近f(x)=0的根,現已知f(x)=x2﹣3,求f(x)=0的一個根的程序框圖如圖所示,則輸出的結果為( )
(n∈N*),則xn+1比xn更靠近f(x)=0的根,現已知f(x)=x2﹣3,求f(x)=0的一個根的程序框圖如圖所示,則輸出的結果為( ) 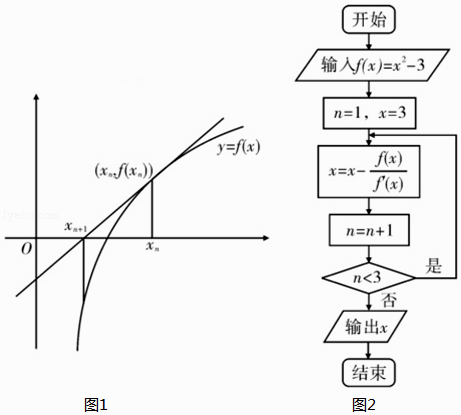
A.2
B.1.75
C.1.732
D.1.73
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的偶函數,且當
上的偶函數,且當![]() 時,
時,![]() .現已畫出函數
.現已畫出函數![]() 在
在![]() 軸左側的圖象,如圖所示,根據圖象:
軸左側的圖象,如圖所示,根據圖象:

(1)請將函數![]() 的圖象補充完整并寫出該函數的增區間(不用證明).
的圖象補充完整并寫出該函數的增區間(不用證明).
(2)求函數![]() 的解析式.
的解析式.
(3)若函數![]() ,求函數
,求函數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() +
+ ![]() .
.
(1)求f(x)≥f(4)的解集;
(2)設函數g(x)=k(x﹣3),k∈R,若f(x)>g(x)對任意的x∈R都成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點O為極點,x軸的正半軸為極軸,且兩個坐標系取相等的長度單位,已知直線l的參數方程為 ![]() (t為參數,0<φ<π),曲線C的極坐標方程為ρcos2θ=8sinθ.
(t為參數,0<φ<π),曲線C的極坐標方程為ρcos2θ=8sinθ.
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)設直線l與曲線C相交于A、B兩點,當φ變化時,求|AB|的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com